题目内容
8．设i为虚数单位，复数z满足$\frac{2i}{z}=1-i$，则复数z等于（ ）| A． | -1-i | B． | 1-i | C． | -1+i | D． | 1+i |
分析 利用复数的运算法则、共轭复数的定义
解答 解：∵复数z满足$\frac{2i}{z}=1-i$，∴z=$\frac{2i}{1-i}$=$\frac{2i（1+i）}{（1-i）（1+i）}$=i-1．
故选：C．
点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
19．设f，g都是由A到A的映射，其对应法则如表所示（从上到下），则与f[g（1）]相同的是（ ）
表1 映射f的对应法则
表2 映射g的对应法则
表1 映射f的对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 4 | 3 | 1 | 2 |
| A． | g[f（3）] | B． | g[f（1）] | C． | f[f（4）] | D． | f[f（3）] |
20．
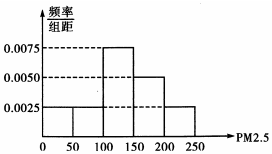PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级
（1）根据样本空气质量PM2.5的数据的频率分布直方图完成下列分布表；
（2）估计该市在下一年的360天中空气质量为一级天气的天数；
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．
PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级| PM2.5 | [0，100） | [100，150） | [150，200） | [200，250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
| PM2.5 | [0，50） | [50，100） | [100，150） | [150，200） | [200，250] |
| 天数 | 5 | 5 | 15 | 10 | 5 |
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．
17．已知△ABC的三个顶点均在抛物线x2=y上，边AC的中线BM∥y轴，|BM|=2，则△ABC的面积为（ ）
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 4 | D． | 8 |
3．
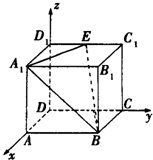如图，在空间直角坐标系D-xyz中，四棱柱ABCD-A1B1C1D1为长方体，AA1=AB=2AD，点E为C1D1的中点，则二面角B1-A1B-E的余弦值为（ ）
如图，在空间直角坐标系D-xyz中，四棱柱ABCD-A1B1C1D1为长方体，AA1=AB=2AD，点E为C1D1的中点，则二面角B1-A1B-E的余弦值为（ ）| A． | $-\frac{{\sqrt{3}}}{3}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
13．若存在两个正实数x，y，使得等式${x^3}{e^{\frac{y}{x}}}-a{y^3}=0$成立，其中e为自然对数的底数，则实数a的取值范围为（ ）
| A． | $[\frac{e^2}{8}，+∞）$ | B． | $（0，\frac{e^3}{27}]$ | C． | $[\frac{e^3}{27}，+∞）$ | D． | $（0，\frac{e^2}{8}]$ |
20．已知y=lnx+x，x∈[1，e]，则y的最大值为（ ）
| A． | 1 | B． | e-1 | C． | e+1 | D． | e |