题目内容
3.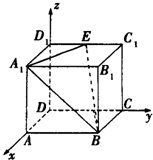 如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )
如图,在空间直角坐标系D-xyz中,四棱柱ABCD-A1B1C1D1为长方体,AA1=AB=2AD,点E为C1D1的中点,则二面角B1-A1B-E的余弦值为( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 分别求出两个平面的法向量,再求出其夹角即可得出结论.
解答 解:设A1(1,0,2),B1(1,2,2),C1(0,2,2),D1(0,0,2),B(1,2,0),
∵E,F分别为C1D1、A1B的中点,∴E(0,1,2),
∴$\overrightarrow{{A}_{1}E}$=(-1,1,0),$\overrightarrow{{A}_{1}B}$=(0,2,-2),
设$\overrightarrow{m}$=(x,y,z)是平面A1BE的一个法向量,
∴$\left\{\begin{array}{l}{-x+y=0}\\{2y-2z=0}\end{array}\right.$,
取x=1,得平面A1BE的一个法向量为$\overrightarrow{m}$=(1,1,1),
又DA⊥平面A1B1B,
∴$\overrightarrow{DA}$=(1,0,0)是平面A1B1B的一个法向量,且二面角B1-A1B-E为锐二面角,
∴二面角B1-A1B-E的余弦值为$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
故选C.
点评 熟练掌握通过建立空间直角坐标系,利用两个平面的法向量的夹角得出二面角的大小的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.设i为虚数单位,复数z满足$\frac{2i}{z}=1-i$,则复数z等于( )
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |