题目内容
20．
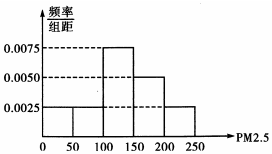PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级| PM2.5 | [0，100） | [100，150） | [150，200） | [200，250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
| PM2.5 | [0，50） | [50，100） | [100，150） | [150，200） | [200，250] |
| 天数 | 5 | 5 | 15 | 10 | 5 |
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．
分析 （1）根据样本空气质量PM2.5的数据的频率分布直方图，能完成分布表．
（2）利用频率分布直方图能估计该市在下一年的360天中空气质量为一级天气的天数．
（3）从一级天气中选2天：a1，a2，从三级天气中选2天：b1，b2，从四级天气中选1天：c1，5天中选2天，利用列举法能求出至少一天是一级天气的概率．
解答 解：（1）根据样本空气质量PM2.5的数据的频率分布直方图，完成下列分布表：
| PM2.5值 | [0，50） | [50，100） | [100，150） | [150，200） | [200，250） |
| 天数 | 5 | 5 | 15 | 10 | 5 |
（2）估计该市在下一年的360天中空气质量为一级天气的天数为：
$\frac{10}{40}×360=90$，
估计某市在下一年的360天中有90天是一级天气．
（3）按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据的比值为：10：10：5=2：2：1，
∴从一级天气中选2天：a1，a2，
从三级天气中选2天：b1，b2，
从四级天气中选1天：c1，
5天中选2天，共有10种选法，分别为：
a1a2，a1b1，a1b2，a1c1，a2b1，a2b2，a2c1，b1b2，b1c1，b2c1，
至少一天是一级天气的情况有7种，
∴至少一天是一级天气的概率p=$\frac{7}{10}$．
点评 本题考查频率分布直方图的应用，考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．
练习册系列答案
相关题目
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F（-1，0），过点F作与x轴垂直的直线与椭圆交于M，N两点，且|MN|=3．
8．设i为虚数单位，复数z满足$\frac{2i}{z}=1-i$，则复数z等于（ ）
| A． | -1-i | B． | 1-i | C． | -1+i | D． | 1+i |
9．三棱柱ABC-A1B1C1中，若三棱锥A1-ABC的体积为9$\sqrt{3}$，则四棱锥A1-B1BCC1的体积为（ ）
| A． | $18\sqrt{3}$ | B． | $24\sqrt{3}$ | C． | 18 | D． | 24 |