题目内容
17.已知△ABC的三个顶点均在抛物线x2=y上,边AC的中线BM∥y轴,|BM|=2,则△ABC的面积为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
分析 作AH⊥BM交BM的延长线于H,求出|BM|,|AH|,即可求得△ABC的面积.
解答 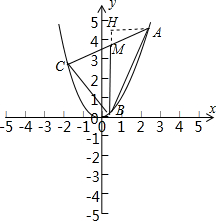 解:根据题意设A(a,a2),B(b,b2),C(c,c2),不妨设a>c,
解:根据题意设A(a,a2),B(b,b2),C(c,c2),不妨设a>c,
∵M为边AC的中点,∴M($\frac{a+c}{2}$,$\frac{{a}^{2}+{c}^{2}}{2}$),
又BM∥y轴,则b=$\frac{a+c}{2}$,
故|BM|=|$\frac{{a}^{2}+{c}^{2}}{2}$-b2|=$\frac{(a-c)^{2}}{4}$=2,
∴(a-c)2=8,即a-c=2$\sqrt{2}$,
作AH⊥BM交BM的延长线于H.
故△ABC的面积为2S△ABM=$2×\frac{1}{2}|BM|•|AH|$=2|a-b|=a-c=2$\sqrt{2}$.
故选B.
点评 本题考查三角形面积的计算,考查抛物线的方程,考查学生的计算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.将y=cosx的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将图象沿x轴负方向平移$\frac{π}{4}$个单位,则所得图象的解析式为( )
| A. | y=sinx | B. | y=-sin2x | C. | $y=cos({2x+\frac{π}{4}})$ | D. | $y=cos({\frac{x}{2}+\frac{π}{4}})$ |
1.A是曲线ρ=3cosθ上任意一点,点A到直线ρcosθ=-1距离的最大值为( )
| A. | $\frac{5}{2}$ | B. | 3 | C. | 4 | D. | 5 |
8.设i为虚数单位,复数z满足$\frac{2i}{z}=1-i$,则复数z等于( )
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F(-1,0),过点F作与x轴垂直的直线与椭圆交于M,N两点,且|MN|=3.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F(-1,0),过点F作与x轴垂直的直线与椭圆交于M,N两点,且|MN|=3.