题目内容
(
)2014=( )
| 1+i |
| 1-i |
| A、i | B、-1 | C、1 | D、-i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的乘方运算法则,化简复数为a+bi的形式即可.
解答:
解:(
)2014=[(
)2]1007=(
)1007=(-1)1007=-1.
故选:B.
| 1+i |
| 1-i |
| 1+i |
| 1-i |
| 2i |
| -2i |
故选:B.
点评:本题考查复数代数形式的混合运算,考查计算能力.

练习册系列答案
相关题目
如图所示,程序框图的输出结果是( )


| A、13 | B、14 | C、16 | D、15 |
下列命题或等式正确的是( )
| A、若f(x)是奇函数,则f(0)=0 | ||
B、∫
| ||
| C、函数f(x)=cos2x是周期为π的减函数 | ||
| D、若a∈R,则“a2<a”是“a>0”的必要条件 |
若实数x,y满足
,则z=
的最小值为( )
|
| y+2 |
| x |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
数列{an}的通项公式为an=(
)2n-4-(
)n-2,则数列{an}( )
| 4 |
| 5 |
| 4 |
| 5 |
| A、有最大项,无最小项 |
| B、有最小项,无最大项 |
| C、既有最大项又有最小项 |
| D、既无最大项又无最小项 |
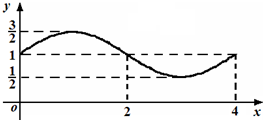
函数f(x)=Asin(ωx+ϕ)+b的图象如图所示,则S=f(0)+f(1)+…+f(2014)等于( )

| A、0 | ||
B、
| ||
C、
| ||
D、
|
