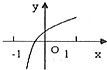题目内容
如图，在四棱锥P-ABCD中，O为AC与BD的交点，AB⊥平面PAD，△PAD是正三角形，DC∥AB，DA=DC=2AB．（1）若点E为棱PA上一点，且OE∥平面PBC，求
| AE |
| PE |
（2）求证：平面PBC⊥平面PDC．
考点：平面与平面垂直的判定,直线与平面平行的性质
专题：空间位置关系与距离
分析：（1）利用线线平行，平行线分线段成比例即可；（2）利用线面垂直，证明面面垂直．
解答：
证 （1）因为OE∥平面PBC，OE?平面PAC，平面PAC∩平面PBC=PC，
所以OE∥PC，
所以AO：OC=AE：EP． …（3分）
因为DC∥AB，DC=2AB，
所以AO：OC=AB：DC=1：2．
所以
=
． …（6分）
（2）法一：取PC的中点F，连结FB，FD．
因为△PAD是正三角形，DA=DC，所以DP=DC．
因为F为PC的中点，所以DF⊥PC．…（8分）
因为AB⊥平面PAD，所以AB⊥PA，AB⊥AD，AB⊥PD．
因为DC∥AB，所以DC⊥DP，DC⊥DA．
设AB=a，在等腰直角三角形PCD中，DF=PF=
a．
在Rt△PAB中，PB=
a．
在直角梯形ABCD中，BD=BC=
a．
因为BC=PB=
a，点F为PC的中点，所以PC⊥FB．
在Rt△PFB中，FB=
a．
在△FDB中，由DF=
a，FB=
a，BD=
a，可知DF2+FB2=BD2，所以FB⊥DF．
…（12分）
由DF⊥PC，DF⊥FB，PC∩FB=F，PC、FB?平面PBC，所以DF⊥平面PBC．
又DF?平面PCD，所以平面PBC⊥平面PDC． …（14分）
法二：取PD，PC的中点，分别为M，F，连结AM，FB，MF，
所以MF∥DC，MF=
DC．
因为DC∥AB，AB=
DC，所以MF∥AB，MF=AB，
即四边形ABFM为平行四边形，所以AM∥BF． …（8分）
在正三角形PAD中，M为PD中点，所以AM⊥PD．
因为AB⊥平面PAD，所以AB⊥AM．
又因为DC∥AB，所以DC⊥AM．
因为BF∥AM，所以BF⊥PD，BF⊥CD．
又因为PD∩DC=D，PD、DC?平面PCD，所以BF⊥平面PCD．…（12分）
因为BF?平面PBC，所以平面PBC?平面PDC．…（14分）
证 （1）因为OE∥平面PBC，OE?平面PAC，平面PAC∩平面PBC=PC，所以OE∥PC，
所以AO：OC=AE：EP． …（3分）
因为DC∥AB，DC=2AB，
所以AO：OC=AB：DC=1：2．
所以
| AE |
| PE |
| 1 |
| 2 |
（2）法一：取PC的中点F，连结FB，FD．
因为△PAD是正三角形，DA=DC，所以DP=DC．
因为F为PC的中点，所以DF⊥PC．…（8分）
因为AB⊥平面PAD，所以AB⊥PA，AB⊥AD，AB⊥PD．
因为DC∥AB，所以DC⊥DP，DC⊥DA．
设AB=a，在等腰直角三角形PCD中，DF=PF=
| 2 |
在Rt△PAB中，PB=
| 5 |
在直角梯形ABCD中，BD=BC=
| 5 |
因为BC=PB=
| 5 |
在Rt△PFB中，FB=
| 3 |
在△FDB中，由DF=
| 2 |
| 3 |
| 5 |
…（12分）
由DF⊥PC，DF⊥FB，PC∩FB=F，PC、FB?平面PBC，所以DF⊥平面PBC．
又DF?平面PCD，所以平面PBC⊥平面PDC． …（14分）
法二：取PD，PC的中点，分别为M，F，连结AM，FB，MF，
所以MF∥DC，MF=
| 1 |
| 2 |
因为DC∥AB，AB=
| 1 |
| 2 |
即四边形ABFM为平行四边形，所以AM∥BF． …（8分）
在正三角形PAD中，M为PD中点，所以AM⊥PD．
因为AB⊥平面PAD，所以AB⊥AM．
又因为DC∥AB，所以DC⊥AM．
因为BF∥AM，所以BF⊥PD，BF⊥CD．
又因为PD∩DC=D，PD、DC?平面PCD，所以BF⊥平面PCD．…（12分）
因为BF?平面PBC，所以平面PBC?平面PDC．…（14分）
点评：本题考查空间直线位置关系，即面面垂直，考查空间想象能力，运算能力和推理论证能力．
练习册系列答案
相关题目
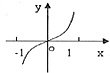
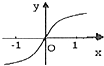
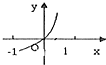
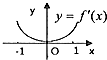已知函数y=f（x）的导函数y=f′（x）的图象如图所示，则下列选项中能表示函数y=f（x）图象的是（ ）
