题目内容
已知集合A={x|2<x≤9},B={x|a≤x<3a}.
(1)当a=2时,求A∩B,A∪B;
(2)若A∪B=A,求a的取值范围;
(3)若A∩B=∅,求a的取值范围.
(1)当a=2时,求A∩B,A∪B;
(2)若A∪B=A,求a的取值范围;
(3)若A∩B=∅,求a的取值范围.
考点:子集与交集、并集运算的转换
专题:集合
分析:(1)a=2时,求出B,然后进行交集、并集的运算即可;
(2)由A∪B=A得B⊆A,B=∅时满足该条件,此时a≥3a,即a≤0;B≠∅时,a需满足
,解该不等式组并合并a≤0即得a的取值范围;
(3)B=∅时满足A∩B=∅,此时a≤0;B≠∅时,要使A∩B=∅则
,或
,解不等式组并合并a≤0的情况即得a的取值范围.
(2)由A∪B=A得B⊆A,B=∅时满足该条件,此时a≥3a,即a≤0;B≠∅时,a需满足
|
(3)B=∅时满足A∩B=∅,此时a≤0;B≠∅时,要使A∩B=∅则
|
|
解答:
解:(1)当a=2时,B={x|2≤x<6},则A∩B={x|2<x<6},A∪B={x|2≤x≤9};
(2)若A∪B=A,则B⊆A,有下列两种情况:
①B=∅,即a≥3a,a≤0;
②当B≠∅时,
,解得:2<a≤3;
∴a的取值范围是(-∞,0]∪(2,3];
(3)①B=∅时,即a≥3a∴a≤0;
②B≠∅时,
,或
,解得:a>9,或0<a≤
;
∴a的取值范围是(-∞,
]∪(9,+∞).
(2)若A∪B=A,则B⊆A,有下列两种情况:
①B=∅,即a≥3a,a≤0;
②当B≠∅时,
|
∴a的取值范围是(-∞,0]∪(2,3];
(3)①B=∅时,即a≥3a∴a≤0;
②B≠∅时,
|
|
| 2 |
| 3 |
∴a的取值范围是(-∞,
| 2 |
| 3 |
点评:考查交集、并集的概念及运算,以及子集、空集的概念,不要漏了B=∅的情况.

练习册系列答案
相关题目
R上可导函数f(x)图象如图所示,则不等式(x2-2x+3)f′(x)>0的解集为( ) 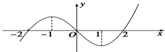

| A、(-∞,-1)∪(1,+∞) |
| B、(-1,1) |
| C、(-∞,-1)∪(-1,0)∪(2,+∞) |
| D、(-∞,-1)∪(-1,1)∪(3,+∞) |
下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
| A、y=x3 | ||
| B、y=|x|+1 | ||
C、f(x)=
| ||
| D、y=20 -|x| |
某校高一、高二、高三三个年级依次有600、500、400名同学,用分层抽样的方法从该校抽取n名同学,其中高一的同学有30名,则n=( )
| A、65 | B、75 | C、50 | D、150 |
设S,T是两个非空集合,且它们互不包含,那么S∪(S∩T)等于( )
| A、S∩T | B、S | C、∅ | D、T |
