题目内容
2.若实数x,y满足x2+y2-2y=0,则$\frac{y-1}{x-2}$的取值范围为( )| A. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | B. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ | C. | $[-\sqrt{3},\sqrt{3}]$ | D. | $({-\sqrt{2},\sqrt{2}})$ |
分析 化圆的一般方程为标准方程,求出圆心坐标和半径,再由$\frac{y-1}{x-2}$的几何意义,即圆上动点与动点(2,1)连线的斜率求解.
解答 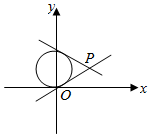 解:化圆x2+y2-2y=0为x2+(y-1)2=1,
解:化圆x2+y2-2y=0为x2+(y-1)2=1,
圆心坐标为(0,1),半径为1.
$\frac{y-1}{x-2}$的几何意义为圆上动点与动点(2,1)连线的斜率.
设过(2,1)与圆x2+(y-1)2=1相切的直线的斜率为k,
直线方程为y-1=k(x-2),即kx-y-2k+1=0.
由点到直线的距离公式得$\frac{|-1-2k+1|}{\sqrt{{k}^{2}+1}}=1$,解得k=$±\frac{\sqrt{3}}{3}$.
∴$\frac{y-1}{x-2}$的取值范围为[$-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}$].
故选:A.
点评 本题考查直线与圆位置关系的应用,考查数学转化思想方法与数形结合的解题思想方法,是中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.如果x-1+yi与i-3x是共轭复数(x,y是实数),则x+y=( )
| A. | -1 | B. | 1 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
17.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)判断是否有95%的把握认为“性别与休闲方式”有关系.
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据以上数据建立一个2×2列联表;
(2)判断是否有95%的把握认为“性别与休闲方式”有关系.
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(Χ2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
14.等比数列{an}中,公比q=2,首项a1=2,函数f(x)=x(x-a1)(x-a2),则f'(0)=( )
| A. | 8 | B. | -8 | C. | 28 | D. | -28 |
