题目内容
9.已知数列{an}满足a1=1,a2=3,且2nan=(n-1)an-1+(n+1)an+1(n≥2且n∈N*)则$\frac{a_n}{n}$的最大值为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{11}{9}$ | D. | $\frac{5}{2}$ |
分析 通过对2nan=(n-1)an-1+(n+1)an+1(n≥2且n∈N*)变形可知nan-(n-1)an-1=(n+1)an+1-nan(n≥2且n∈N*),进而可知数列{nan}是首项为1、公差为5的等差数列,进而可知$\frac{{a}_{n}}{n}$=$\frac{5n-4}{{n}^{2}}$=$\frac{5-\frac{4}{n}}{n}$=(5-$\frac{4}{n}$)•$\frac{1}{n}$,利用函数f(x)=(5-4x)x的单调性计算可得结论.
解答 解:因为2nan=(n-1)an-1+(n+1)an+1(n≥2且n∈N*),
所以nan-(n-1)an-1=(n+1)an+1-nan(n≥2且n∈N*),
又因为a1=1,a2=3,
所以(n+1)an+1-nan=nan-(n-1)an-1=…=2a2-a1=5,
所以数列{nan}是首项为1、公差为5的等差数列,
所以nan=1+5(n-1)=5n-4,
所以$\frac{{a}_{n}}{n}$=$\frac{5n-4}{{n}^{2}}$=$\frac{5-\frac{4}{n}}{n}$=(5-$\frac{4}{n}$)•$\frac{1}{n}$,
记f(x)=(5-4x)x,则函数y=f(x)图象是关于x=$\frac{5}{8}$对称、开口向下的抛物线,
由于0<x≤1,所以f(x)max=f($\frac{5}{8}$)=$\frac{25}{16}$,
由于n∈N*,所以当n=2时$\frac{{a}_{n}}{n}$取得最大值$\frac{3}{2}$,
故选:B.
点评 本题考查数列的通项,考查运算求解能力,构造新数列是解决本题的关键,注意解题方法的积累,属于中档题.

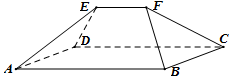 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )| A. | $8\sqrt{3}$ | B. | $8+8\sqrt{3}$ | C. | $6\sqrt{2}+2\sqrt{3}$ | D. | $8+6\sqrt{2}+2\sqrt{3}$ |
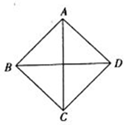 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$+2 | D. | 4$\sqrt{3}$+2 |
| A. | $\frac{13}{25}$ | B. | $\frac{12}{25}$ | C. | $\frac{13}{20}$ | D. | $\frac{3}{5}$ |