题目内容
19.若等比数列{an}的各项均为正数,a1+$\frac{2}{3}{a}_{2}$=3,a42=$\frac{1}{9}{a}_{3}{a}_{7}$,则a4=27.分析 利用等比数列的通项公式及其性质即可得出.
解答 解:设等比数列{an}的公比为q>0,
∵a42=$\frac{1}{9}{a}_{3}{a}_{7}$,∴9${a}_{4}^{2}$=${a}_{5}^{2}$,∴3a4=a5.
解得q=3.
代入a1+$\frac{2}{3}{a}_{2}$=3,可得:${a}_{1}(1+\frac{2}{3}×3)$=3,解得a1=1.
则a4=33=27.
故答案为:27.
点评 本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
9.已知数列{an}满足a1=1,a2=3,且2nan=(n-1)an-1+(n+1)an+1(n≥2且n∈N*)则$\frac{a_n}{n}$的最大值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{11}{9}$ | D. | $\frac{5}{2}$ |
7.如图为某市2017年2月28天的日空气质量指数折线图.
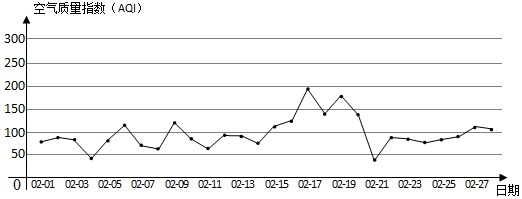
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
(Ⅰ)请根据所给的折线图补全下方的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
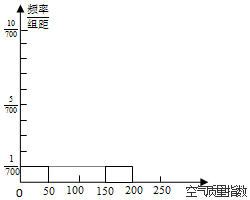
(Ⅱ)研究人员发现,空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系,以100ug/m3为单位,如表给出PM2.5与CO的相关数据:
求y关于x的回归方程,并估计当CO排放量是200ug/m3时,PM2.5的值.
(用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$)

由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |

(Ⅱ)研究人员发现,空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系,以100ug/m3为单位,如表给出PM2.5与CO的相关数据:
| CO(x) | 0.5 | 1 | 1.5 |
| PM2.5(y) | 1 | 2 | 4 |
(用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$)
11.复数$\frac{(1+i)^{2}}{2i}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |