题目内容
已知非负数a、b、c满足a+b+c=1，证明：
+
+
≤
．
| ab |
| c+1 |
| bc |
| a+1 |
| ca |
| b+1 |
| 1 |
| 4 |
考点：综合法与分析法(选修）,不等式的证明
专题：证明题,不等式的解法及应用
分析：通过重要不等式，a2+b2≥2ab证明
≤
(
+
)，类似推出所证明不等式左侧的两个表达式，可以综合法证明即可．
| ab |
| c+1 |
| 1 |
| 4 |
| ab |
| a+c |
| ab |
| b+c |
解答：
解：∵非负数a、b、c满足a+b+c=1，
又a2+b2≥2ab，∴a2+b2+4c2+2ab+4bc+4ac≥4c2+4ab+4bc+4ac，
即（a+b+2c）2≥4（c2+ab+bc+ac）=4（a+c）（b+c），
∴
≤
•
=
（
+
），
可得
≤
(
+
)，
即
≤
(
+
)，
同理
≤
(
+
)，
≤
(
+
)，
∴
+
+
≤
(
+
+
+
+
+
)=
(a+b+c)=
，
∴
+
+
≤
．
又a2+b2≥2ab，∴a2+b2+4c2+2ab+4bc+4ac≥4c2+4ab+4bc+4ac，
即（a+b+2c）2≥4（c2+ab+bc+ac）=4（a+c）（b+c），
∴
| 1 |
| a+b+2c |
| 1 |
| 4 |
| a+b+2c |
| (a+c)(b+c) |
| 1 |
| 4 |
| 1 |
| a+c |
| 1 |
| b+c |
可得
| ab |
| a+b+2c |
| 1 |
| 4 |
| ab |
| a+c |
| ab |
| b+c |
即
| ab |
| c+1 |
| 1 |
| 4 |
| ab |
| a+c |
| ab |
| b+c |
同理
| bc |
| a+1 |
| 1 |
| 4 |
| bc |
| b+a |
| cb |
| c+a |
| ac |
| b+1 |
| 1 |
| 4 |
| ca |
| a+b |
| ca |
| b+c |
∴
| ab |
| c+1 |
| bc |
| a+1 |
| ca |
| b+1 |
| 1 |
| 4 |
| ab |
| a+c |
| ab |
| b+c |
| bc |
| b+a |
| cb |
| c+a |
| ca |
| a+b |
| ca |
| b+c |
| 1 |
| 4 |
| 1 |
| 4 |
∴
| ab |
| c+1 |
| bc |
| a+1 |
| ca |
| b+1 |
| 1 |
| 4 |
点评：本题考查不等式的证明，综合法的应用，解题的关键是分析所证明不等式的左侧形式，开学分析问题解决问题的能力．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图，四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，平面PAB⊥平面ABCD，PA=PB=2AB．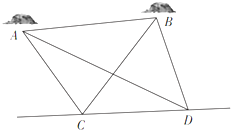
如图，A，B是海平面上的两个小岛，为测量A，B两岛间的距离，测量船以15海里/小时的速度沿既定直线CD航行，在t1时刻航行到C处，测得∠ACB=75°，∠ACD=120°，1小时后，测量船到达D处，测得∠ADC=30°，∠ADB=45°，求A，B两小岛间的距离．（注：A、B、C、D四点共面）
在直角梯形ABCD中，AD∥BC，
如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，且AB=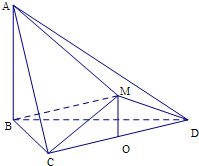
如图，△BCD与△MCD都是边长为2的正三角形，O是CD的中点，平面MCD⊥平面BCD，AB⊥平面BCD，AB=2