题目内容
4.已知$\overrightarrow{e_1},\overrightarrow{e_2}$是平面内两个不共线的非零向量,$\overrightarrow{AB}=2\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{BE}=-\overrightarrow{e_1}+λ\overrightarrow{e_2}$,$\overrightarrow{EC}=-2\overrightarrow{e_1}+\overrightarrow{e_2}$,且A,E,C三点共线.(1)求实数λ的值;
(2)已知$\overrightarrow{e_1}$=(2,1),$\overrightarrow{e_2}$=(2,-2),点D(3,5),若A,B,C,D四点按逆时针顺序构成平行四边形,求点A的坐标.
分析 (1)可以利用三点共线,得到向量的线性关系,解出λ的值,得到本题结论,
(2)由已知几何条件得到向量间关系,再坐标化得到A点的坐标,即本题答案.
解答 解:(1)$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)+(-$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$)=$\overrightarrow{{e}_{1}}$+(1+λ)$\overrightarrow{{e}_{2}}$.
∵A,E,C三点共线,
∴存在实数k,使得$\overrightarrow{AE}$=k$\overrightarrow{EC}$,
即$\overrightarrow{{e}_{1}}$+(1+λ)$\overrightarrow{{e}_{2}}$=k(-2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$),
得(1+2k)$\overrightarrow{{e}_{1}}$=(k-1-λ)$\overrightarrow{{e}_{2}}$.
∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是平面内两个不共线的非零向量,
∴$\left\{\begin{array}{l}{1+2k=0}\\{λ=k-1}\end{array}\right.$,解得k=-$\frac{1}{2}$,λ=-$\frac{3}{2}$.
(2)$\overrightarrow{BC}$=$\overrightarrow{BE}$+$\overrightarrow{EC}$=-3$\overrightarrow{{e}_{1}}$-$\frac{1}{2}$$\overrightarrow{{e}_{2}}$
=(-6,-3)+(-1,1)=(-7,-2).
∵A,B,C,D四点按逆时针顺序构成平行四边形,
∴$\overrightarrow{AD}$=$\overrightarrow{BC}$.
设A(x,y),则$\overrightarrow{AD}$=(3-x,5-y),
∵$\overrightarrow{BC}$=(-7,-2),
∴$\left\{\begin{array}{l}{3-x=-7}\\{5-y=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=10}\\{y=7}\end{array}\right.$,即点A的坐标为(10,7).
点评 本题考查了向量共线和向量的坐标运算,本题难度不大,属于基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 有过粉尘环境工作经历 | 无粉尘环境工作经历 | 合计 | |
| 有尘肺病 | 22 | 2 | 24 |
| 无尘肺病 | 898 | 1498 | 2396 |
| 合计 | 920 | 1500 | 2420 |
| A. | (0,1) | B. | (1,10) | C. | (1,+∞) | D. | (10,+∞) |
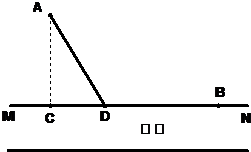 有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?
有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?