题目内容
10.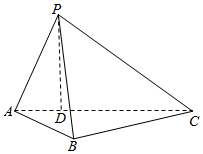 如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.
如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.(1)求三棱锥P-ABC的体积;
(2)证明:△PBC为直角三角形.
分析 (1)由平面PAC⊥平面ABC,PD⊥AC,得PD⊥平面ABC,取AC边上的中点为E,有BE⊥AC.求出BE和AC的长度,可得△ABC的面积,然后代入体积公式求得三棱锥P-ABC的体积;
(2)由PD⊥AC,得△PCD为直角三角形,求解得到PC=5,连接BD,在Rt△BDE中,求得BD=2,在Rt△PBD中,求得$PB=\sqrt{13}$,然后利用勾股定理可得BC2+PB2=PC2.得到△PBC为直角三角形.
解答 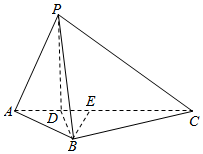 (1)解:∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD?平面PAC,PD⊥AC,
(1)解:∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD?平面PAC,PD⊥AC,
∴PD⊥平面ABC
记AC边上的中点为E,在△ABC中,
∵AB=AC,
∴BE⊥AC.
∵$AB=BC=2\sqrt{3}$,AC=AD+DC=6,
∴$BE=\sqrt{(2\sqrt{3})^{2}-{3}^{2}}=\sqrt{3}$,
∴△ABC的面积$S=\frac{1}{2}AC×BE=3\sqrt{3}$,
∵PD=3,
∴三棱锥P-ABC的体积${V}_{P-ABC}=\frac{1}{3}×{S}_{△ABC}×PD$=$\frac{1}{3}×3\sqrt{3}×3=3\sqrt{3}$;
(2)证明:∵PD⊥AC,
∴△PCD为直角三角形.
∵PD=3,CD=4,
∴PC=5,
连接BD,在Rt△BDE中,
∵∠BED=90°,$BE=\sqrt{3}$,DE=1,
∴BD=2,
由(1)知PD⊥平面ABC,又BD?平面ABC,
∴PD⊥BD.
在Rt△PBD中,∵PD=3,BD=2,
∴$PB=\sqrt{13}$,
在△PBC中,∵$BC=2\sqrt{3}$,$PB=\sqrt{13}$,PC=5,
∴BC2+PB2=PC2.
∴△PBC为直角三角形.
点评 本题考查棱锥体积的求法,考查了空间中线面位置关系的判定,考查空间想象能力和思维能力,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |

 B.
B. C.
C.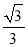 D.
D.
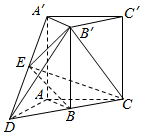 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.