题目内容
12．已知数列{an}满足an+1=$\sqrt{{a}_{n}^{2}+4}$，且a1=1，数列bn=${a}_{n}^{2}$，则{bn}的前n项和Sn=2n2-n．分析 由数列递推式可得{bn}是以1为首项，以4为公差的等差数列，然后代入等差数列的前n项和得答案．
解答 解：由an+1=$\sqrt{{a}_{n}^{2}+4}$，得${{a}_{n+1}}^{2}-{{a}_{n}}^{2}=4$，
又bn=${a}_{n}^{2}$，∴bn+1-bn=4，
且${b}_{1}={{a}_{1}}^{2}=1$，
∴{bn}是以1为首项，以4为公差的等差数列，
则Sn=n×1+$\frac{n（n-1）×4}{2}$=2n2-n．
故答案为：2n2-n．
点评 本题考查数列递推式，考查了等差关系的确定，训练了等差数列前n项和公式的应用，是中档题．
练习册系列答案
相关题目
与圆
相交于
两点，若
，则
的取值范围是______．
1．
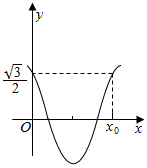已知函数f（x）=2cos（πx）•cos2$\frac{φ}{2}$-sin（πx）•sinφ-cos（πx）（0≤φ＜$\frac{π}{2}$）的部分图象如图所示，则图中的x0的值为（ ）
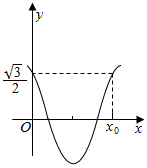已知函数f（x）=2cos（πx）•cos2$\frac{φ}{2}$-sin（πx）•sinφ-cos（πx）（0≤φ＜$\frac{π}{2}$）的部分图象如图所示，则图中的x0的值为（ ）| A． | $\frac{5}{6}$ | B． | $\frac{5}{4}$ | C． | $\frac{5}{2}$ | D． | $\frac{5}{3}$ |