题目内容
设
=（3，1），
=（-1，2），
⊥
，
∥
（O为坐标原点）
（1）求点C的坐标；
（2）若
+
=
，求
的坐标．
| OA |
| OB |
| OC |
| OB |
| BC |
| OA |
（1）求点C的坐标；
（2）若
| OD |
| OA |
| OC |
| OD |
考点：平面向量共线（平行）的坐标表示,平面向量的坐标运算
专题：平面向量及应用
分析：（1）利用向量垂直与数量积的关系、向量共线定理即可得出；
（2）利用向量坐标运算即可得出．
（2）利用向量坐标运算即可得出．
解答：
解：（1）设C（x，y），
=（x+1，y-2）．
∵
⊥
，
∥
（O为坐标原点），
∴-x+2y=0，x+1-3（y-2）=0，
解得y=7，x=14．
∴（14，7），
（2）∵
+
=
，
∴
=
-
=（14，7）-（3，1）=（11，6）．
| BC |
∵
| OC |
| OB |
| BC |
| OA |
∴-x+2y=0，x+1-3（y-2）=0，
解得y=7，x=14．
∴（14，7），
（2）∵
| OD |
| OA |
| OC |
∴
| OD |
| OC |
| OA |
点评：本题考查了向量垂直与数量积的关系、向量共线定理、向量坐标运算，属于基础题．
练习册系列答案
相关题目
对?x1∈[1，2]，?x2∈[2，3]总有2ax12-x22+2x1x2+4x12（lnx2-lnx1）≥0成立，则实数a的取值范围（ ）
A、[-
| ||||
B、（-∞，
| ||||
C、[-
| ||||
D、[
|
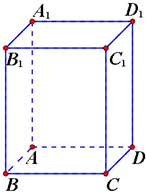长方体ABCD-A1B1C1D1中，宽、长、高分别为3、4、5，现有一个小虫从A出发沿长方体表面爬行到C1来获取食物，求其路程的最小值．