题目内容
4.如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=2,四棱锥P-ABCD的五个顶点都在一个球面上,则这个球的表面积是12π.分析 把四棱锥补成正四棱柱,根据正四棱柱的对角线长等于球的直径求得外接球的半径,代入球的表面积公式计算.
解答 解:由题意,把四棱锥补成正四棱柱,则四棱锥的外接球是正四棱柱的外接球,
∵正四棱柱的对角线长等于球的直径,
∴2R=$\sqrt{3}$•2=2$\sqrt{3}$,
∴R=$\sqrt{3}$,
外接球的表面积S=4πR2=12π.
故答案为:12π.
点评 本题考查了棱锥的外接球的表面积的求法,利用正四棱柱的对角线长等于球的直径求得外接球的半径是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
14.已知A,B分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,不同两点P,Q在双曲线C上,且关于x轴对称,设直线AP,BQ的斜率分别为λ,μ,则当$\frac{16}{λμ}$+λμ取最大值时,双曲线C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
15.已知$\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(6,y),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则y等于( )
| A. | -9 | B. | -4 | C. | 4 | D. | 9 |
12.定义R上的减函数f(x),其导函数f'(x)满足$\frac{f(x)}{f'(x)}<1-x$,则下列结论正确的是( )
| A. | 当且仅当x∈(-∞,1),f(x)<0 | B. | 当且仅当x∈(1,+∞),f(x)>0 | ||
| C. | 对于?x∈R,f(x)<0 | D. | 对于?x∈R,f(x)>0 |
16.复数z1=2+i,若复数z1,z2在复平面内的对应点关于虚轴对称,则z1z2=( )
| A. | -5 | B. | 5 | C. | -3+4i | D. | 3-4i |
7.某几何体的三视图如图所示,则其体积为( )


| A. | 80 | B. | 160 | C. | 240 | D. | 480 |
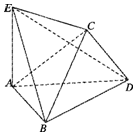 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.