题目内容
15．已知$\overrightarrow{a}$=（3，2），$\overrightarrow{b}$=（6，y），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则y等于（ ）| A． | -9 | B． | -4 | C． | 4 | D． | 9 |
分析 根据题意，由向量平行的坐标表示方法，可得3y=2×6，解可得y的值，即可得答案．
解答 解：根据题意，$\overrightarrow{a}$=（3，2），$\overrightarrow{b}$=（6，y），
若$\overrightarrow{a}$∥$\overrightarrow{b}$，则有3y=2×6，
解可得y=4；
故选：C．
点评 本题考查向量平行的坐标表示方法，关键是掌握向量的坐标表示方法．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
5．若复数z满足z（4-i）=5+3i（i为虚数单位），则复数z的共轭复数为（ ）
| A． | 1-i | B． | -1+i | C． | 1+i | D． | -1-i |
3．
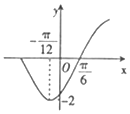设函数f（x）=cos2x-$\sqrt{3}$sin2x，把y=f（x）的图象向左平移$φ（{|φ|＜\frac{π}{2}}）$个单位后，得到的部分图象如图所示，则f（φ）的值等于（ ）
设函数f（x）=cos2x-$\sqrt{3}$sin2x，把y=f（x）的图象向左平移$φ（{|φ|＜\frac{π}{2}}）$个单位后，得到的部分图象如图所示，则f（φ）的值等于（ ）| A． | $-\sqrt{3}$ | B． | $\sqrt{3}$ | C． | -1 | D． | 1 |
10．已知等差数列{an}的前n项和为Sn，且3a3=a6+4，若S5＜10，则a2的取值范围是（ ）
| A． | （-∞，2） | B． | （-∞，0） | C． | （1，+∞） | D． | （0，2） |
20．已知函数f（x）=x$（{{e^x}-\frac{1}{e^x}}）$，若f（x1）＜f（x2），则（ ）
| A． | x1＞x2 | B． | x1＜x2 | C． | ${x}_{1}^{2}$＜${x}_{2}^{2}$ | D． | x1+x2=0 |
7．已知命题P：若△ABC为钝角三角形，则sinA＜cosB；命题q：?x，y∈R，若x+y≠2，则x≠-1或y≠3，则下列命题为真命题的是（ ）
| A． | p∨（?q） | B． | （?p）∧q | C． | p∧q | D． | （?p）∧（?q） |