题目内容

8．已知椭圆C：$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1，点M与C的焦点不重合，若M关于C的焦点的对称点分别为A，B，点M关于椭圆C上任意一动点的对称点为N，则|AN|+|BN|=20．

分析 根据已知条件，作出图形，MN的中点连接椭圆的两个焦点，便会得到三角形的中位线，根据中位线的性质及椭圆上的点到两焦点的距离和为2a即可求出|AN|+|BN|．

解答 解：椭圆C：$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1，a=5，b=4，c=3
设MN的中点为Q，椭圆C的左右焦点分别为F1，F2，
如图，连接QF1，QF2，
∵F1是MA的中点，Q是MN的中点，
∴F1Q是△MAN的中位线；
丨QF1丨=$\frac{1}{2}$丨AN丨，
同理：丨QF2丨=$\frac{1}{2}$丨NB丨，
∵Q在椭圆C上，
∴|QF1|+|QF2|=2a=10，
∴|AN|+|BN|=2（|QF1|+|QF2|）=20．
故答案为20．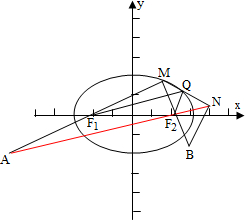

点评 本题考查椭圆的定义，椭圆的基本性质的应用，三角形的中位线定理，属于中档题．

练习册系列答案
相关题目
18．已知m，n为两条直线，α，β为两个不同的平面，则下列说法正确的是（　　）
A．若m∥α，α∥β，则m∥βB．若α⊥β，m?α，则m⊥β
C．若m⊥α，m∥n，α⊥β，则n∥βD．若m⊥α，m∥n，α∥β，则n⊥β
19．向量a=（2，-2），b=（4，x）且a，b共线，则x的值为（　　）
A．1B．-1C．-3D．-4
16．函数$f（x）=（{1-\frac{2}{{1+{2^x}}}}）tanx$的图象（　　）
A．关于x轴对称B．关于y轴对称C．关于y=x轴对称D．关于原点轴对称
3．已知函数f（x）为R上的偶函数，g（x）为R上的奇函数，且f（x）+g（x）=log4（4x+1）．
（1）求f（x），g（x）的解析式；
（2）若函数h（x）=f（x）-$\frac{1}{2}{log_2}（{a•{2^x}+2\sqrt{2}a}）（{a＞0}）$在R上只有一个零点，求实数a的取值范围．
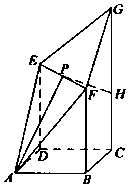13．如图，四边形ABCD是边长为$\sqrt{2}$的正方形，CG⊥平面ABCD，DE∥BF∥CG，DE=BF=$\frac{3}{5}$CG．P为线段EF的中点，AP与平面ABCD所成角为60°．在线段CG上取一点H，使得GH=$\frac{3}{5}$CG．
（1）求证：PH⊥平面AEF；
（2）求二面角A-EF-G的余弦值．
20．某市为了制定合理的节电方案，供电局对居民用电进行了调查，通过抽样，获得了某年200户居民每户的月均用电量（单位：度），将数据按照[0，100），[100，200），[200，300），[300，400），[400，500），[500，600），[600，700），[700，800），[800，900]分成9组，制成了如图所示的频率分布直方图．

（Ⅰ）求直方图中m的值并估计居民月均用电量的中位数；
（Ⅱ）现从第8组和第9组的居民中任选取2户居民进行访问，则两组中各有一户被选中的概率．
17．已知等比数列{an}中，各项都是正数，且3a1，$\frac{1}{2}$a3，2a2成等差数列，则等比数列{an}公比q等于（　　）
A．3B．9C．27D．81
18．如图，在几何体A1B1D1-ABCD中，四边形A1B1BA与A1D1DA均为直角梯形，且AA1⊥底面ABCD，四边形ABCD为正方形，AB=2A1D1=2A1B1=4，AA1=4，P为DD1的中点．
（Ⅰ）求证：AB1⊥PC；
（Ⅱ）求平面B1CD1与平面PBC所成的锐二面角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网