题目内容
18.已知${({1-2x})^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$,则|a0|+|a1|+|a2|+…+|a7|=2187.分析 利用二项展开式的通项公式求出二项展开式的通项,判断出展开式各项系数的符号,将绝对值去掉,给二项式中的x赋值-1求出|a0|+|a1|+|a2|+…+|a7|的值
解答 解:二项展开式的通项为Tr+1=C7r(-x)r=(-2)rC7rxr
∴|a0|+|a1|+|a2|+…+|a7|=a0-a1+a2-…-a7
令二项式的x=-1得
37=a0-a1+a2-…-a7
∴|a0|+|a1|+|a2|+…+|a7|=2187
故答案为:2187
点评 解决二项展开式的特定项问题一般利用的工具是二项展开式的通项公式;解决二项展开式的系数和问题一般利用赋值的方法.

练习册系列答案
相关题目
8.函数f(x)=3x+$\frac{12}{x^2}$(x>0)取得最小值时x为( )
| A. | 8 | B. | 9 | C. | 2 | D. | 6$\sqrt{6}$ |
6.如图,小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )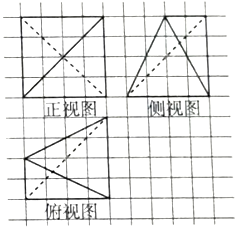

| A. | 8$\sqrt{3}$ | B. | $\frac{80}{3}$ | C. | 16$\sqrt{3}$ | D. | 32 |
13.已知O、A、B是平面上的三个点,直线AB上有一个点C,满足$2\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow 0$,则$\overrightarrow{OC}$=( )
| A. | $-\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$ | B. | $\frac{2}{3}\overrightarrow{OA}-\frac{1}{3}\overrightarrow{OB}$ | C. | $-\overrightarrow{OA}+2\overrightarrow{OB}$ | D. | $2\overrightarrow{OA}-\overrightarrow{OB}$ |
7.设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )
| A. | 0,$\frac{1}{2}$,0,0,$\frac{1}{2}$ | B. | 0.1,0.2,0.3,0.4 | ||
| C. | p,1-p(0≤p≤1) | D. | $\frac{1}{1×2}$,$\frac{1}{2×3}$,…,$\frac{1}{7×8}$ |