题目内容

设命题p：函数f（x）=3x2-2ax-1在区间（-∞，1]上单调递减；命题q：函数y=
x2+ax+1
的定义域是R，如果命题“p或q”为真命题，“p且q”为假命题，求实数a的取值范围．
考点：复合命题的真假
专题：函数的性质及应用,简易逻辑
分析：p为真命题?f（x）图象的对称轴x=
a
3
≥1．q为真命题?△=a2-4≤0恒成立．命题“p或q”为真命题，“p且q”为假命题，可知：p和q有且只有一个是真命题．
解答： 解：p为真命题?f（x）图象的对称轴x=
a
3
≥1?a≥3．
q为真命题?△=a2-4≤0恒成立?-2≤a≤2．
∵命题“p或q”为真命题，“p且q”为假命题，
∴p和q有且只有一个是真命题．
p真q假?
a≥3
a＜-2或a＞2
?a≥3；
p假q真?
a＜3
-2≤a≤2
?-2≤a≤2
综上所述：a∈[-2，2]∪[3，+∞）．
点评：本题考查了二次函数的性质、复合命题真假的判定方法，考查了推理能力和计算能力，属于基础题．
练习册系列答案
相关题目
已知△ABC的面积为S，且
AB
•
BC
=1，若
1
2
＜S＜
3
2
，则∠ABC的范围是（　　）
A、（
π
6
，
π
3
）
B、（
π
4
，
π
3
）
C、（
2π
3
，
5π
6
）
D、（
2π
3
，
3π
4
）
如图，在三棱柱ABC-A1B1C1中，AB⊥AC，顶点A1在底面ABC上的射影恰为点B，且AB=AC=A1B=2．
（1）求证：A1C1⊥平面AA1B1B；
（2）若P为线段B1C1的中点，求四棱锥P-AA1B1B的体积．
设函数f（x）=mlnx，h（x）=x-a．
（Ⅰ）当a=0时，f（x）≤h（x）在（1，+∞）上恒成立，求实数m的取值范围；
（Ⅱ）当m=2时，若函数k（x）=f（x）-h（x）在[1，3]上恰有两个不同零点，求实数a的取值范围；
（Ⅲ）证明：当n≥2，n∈N*时，log2e+log3e+log4e+…+logne＞
3n2-n-2
2n(n+1)
．
已知函数f（x）的定义域为（0，+∞），当x＞1时，f（x）＞0，且对于任意的x，y∈（0，+∞），恒有f（xy）=f（x）+f（y）成立．
（Ⅰ）求f（1）；
（Ⅱ）证明：函数f（x）在（0，+∞）上单调递增；
（Ⅲ）当f（2）=1时，
①解不等式f（x）+f（x-3）≤2；
②求函数f（x）在[
2
，4]上的值域．
已知向量
a
=（1，cosx），
b
=（1，siny），
c
=（4，1），且（
a
+
b
）∥
c

（1）若x=
π
2
，求|
b
|；
（2）求
b
•
c
-
a
2的最值．
求与曲线y=
3x2
在点P（8，4）处的切线垂直的直线方程．
已知命题p：曲线
x2
a-1
+
y2
5-a
=1为焦点在x轴上的椭圆；命题q：函数f（x）=x2-ax+9在R上取值恒为正；若命题“p或q”为真，命题“p且q”为假，求实数a的取值范围．
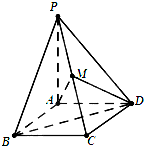在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥平面ABCD，PA=1，点M是棱PC的中点．
（1）求证：PB⊥面AMD；
（2）求三棱锥C-AMD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网