题目内容
12.若抛物线x2=2py(p>0)的焦点在圆x2+y2+2x-1=0上,则这条抛物线的准线方程为y=-1.分析 求出圆x2+y2+2x-1=0与y轴正半轴的交点坐标,可得抛物线的焦点坐标,则答案可求.
解答 解:由x2+y2+2x-1=0,取x=0,得y2=1,即y=±1,
∵抛物线x2=2py(p>0)的焦点在圆x2+y2+2x-1=0上,
∴可得抛物线x2=2py(p>0)的焦点坐标为(0,1),则$\frac{p}{2}=1$,
∴抛物线x2=2py(p>0)的准线方程为y=-$\frac{p}{2}=-1$.
故答案为:y=-1.
点评 本题考查抛物线的简单性质,考查圆与圆锥曲线位置关系的应用,是中档题.

练习册系列答案
相关题目
7.点A(sin2016°,cos2016°)在直角坐标平面上位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.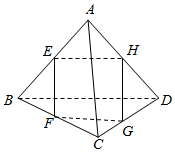 在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
 在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )| A. | 2对 | B. | 4对 | C. | 6对 | D. | 8对 |
4.向量$\overrightarrow{a}$=(1,2,3),则|$\overrightarrow{a}$|=( )
| A. | $\sqrt{15}$ | B. | $\sqrt{14}$ | C. | $\sqrt{13}$ | D. | $\sqrt{12}$ |
2.椭圆的两个焦点和短轴的两个端点,恰好是含60°角的菱形的四个顶点,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$或$\frac{\sqrt{3}}{3}$ |
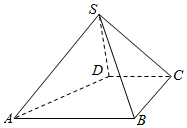 如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.