题目内容
20．执行如图的程序框图，则输出的S的值为（ ）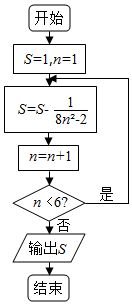
| A． | $\frac{7}{9}$ | B． | $\frac{17}{22}$ | C． | $\frac{10}{13}$ | D． | $\frac{23}{30}$ |
分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
解答 解：第一次执行循环体后，S=$\frac{5}{6}$，n=2，满足进行循环的条件，
第二次执行循环体后，S=$\frac{4}{5}$，n=3，满足进行循环的条件，
第三次执行循环体后，S=$\frac{11}{14}$，n=4，满足进行循环的条件，
第四次执行循环体后，S=$\frac{7}{9}$，n=5，满足进行循环的条件，
第五次执行循环体后，S=$\frac{17}{22}$，n=6，不满足进行循环的条件，
故输出的S值为$\frac{17}{22}$，
故选：B
点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．
练习册系列答案
相关题目
△ABC中，AB=1，AC=2．
11．已知集合A={3，$\sqrt{a}$}，B={a，b}，若A∩B={2}，则A∪B=（ ）
| A． | {2，3} | B． | {3，4} | C． | {$\sqrt{2}$，2，3} | D． | {2，3，4} |
8．已知二次函数f（x）=ax2+bx+c的导数为f′（x），f′（0）＞0，对于任意的实数x都有f（x）≥0，则$\frac{f（1）}{{{f^'}（0）}}$的取值范围是（ ）
| A． | $[\frac{3}{2}，+∞）$ | B． | [2，+∞） | C． | $[\frac{5}{2}，+∞）$ | D． | [3，+∞） |
15．计算：$\int_1^3{（2x-\frac{1}{x^2}}）dx$=（ ）
| A． | $\frac{22}{3}$ | B． | $\frac{26}{3}$ | C． | $\frac{34}{3}$ | D． | $-\frac{2}{27}$ |
9．使得函数y=3-cosx取得最大值的x的集合是（ ）
| A． | {x|x=2kπ，k∈Z} | B． | {x|x=π+2kπ，k∈Z} | C． | {x|x=-$\frac{π}{2}$+2kπ，k∈Z} | D． | {x|x=$\frac{π}{2}$+2kπx，k∈Z} |