题目内容
1．在△ABC中，b=17，c=24，B=45°，则此三角形解的情况是（ ）| A． | 一解 | B． | 两解 | C． | 一解或两解 | D． | 无解 |
分析 由csinB＜b，即可得出解的情况．
解答 
解：过点A作AD⊥BD．点D在∠B的一条边上，
∵h=csinB=12$\sqrt{2}$＜17=b=AC，
因此此三角形两解．
故选：B．
点评 本题考查了正弦定理解三角形，考查了推理能力与计算能力，属于中档题．
练习册系列答案
初中学业考试导与练系列答案
相关题目
11．函数y=logax（x＞0）且a≠1）的图象经过点（2$\sqrt{2}$，-1），函数y=bx（b＞0）且b≠1）的图象经过点（1，2$\sqrt{2}$），则下列关系式中正确的是（ ）
| A． | a2＞b2 | B． | 2a＞2b | C． | （$\frac{1}{2}$）a＞（$\frac{1}{2}$）b | D． | a${\;}^{\frac{1}{2}}$＞b${\;}^{\frac{1}{2}}$ |
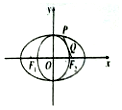如图，F1，F2是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右两焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q是线段PF2的中点，则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$（e为椭圆的离心率）的最小值为$\frac{\sqrt{5}}{3}$．
11．直线4x-3y=0与圆（x-1）2+（y-3）2=10相交所得弦长为（ ）
| A． | 6 | B． | 3 | C． | $6\sqrt{2}$ | D． | $3\sqrt{2}$ |