题目内容
12.命题“对任意$x∈[0,\frac{π}{4}]$,tanx<m恒成立”是假命题,则实数m取值范围是(-∞,1].分析 由x的范围求出tanx的范围,再由tanx<m恒成立求出m的范围,结合补集思想求得命题“对任意$x∈[0,\frac{π}{4}]$,tanx<m恒成立”是假命题的m的取值范围.
解答 解:当$x∈[0,\frac{π}{4}]$时,tanx∈[0,1],
若tanx<m恒成立,则m>1.
∵命题“对任意$x∈[0,\frac{π}{4}]$,tanx<m恒成立”是假命题,
∴m≤1.
∴实数m取值范围是(-∞,1].
故答案为:(-∞,1].
点评 本题考查命题的真假判断与应用,考查恒成立问题的求解方法,体现了补集思想在解题中的应用,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.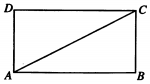 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
1.在△ABC中,b=17,c=24,B=45°,则此三角形解的情况是( )
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |