题目内容
6.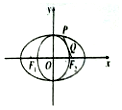 如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$.
如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$.
分析 连接PF1,OQ,运用中位线定理可得|F1P|=2|OQ|=2b,由椭圆的定义可得|PF1|+|PF2|=2a,可得|PF2|=2a-2b,运用勾股定理,化简可得3b=2a,e=$\frac{\sqrt{5}}{3}$,求得${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$=$\frac{1}{2}$(a+$\frac{5}{9a}$),运用基本不等式即可得到最小值.
解答 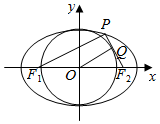 解:连接F1P,OQ,因为点Q为线段PF2的中点,所以|F1P|=2|OQ|=2b,
解:连接F1P,OQ,因为点Q为线段PF2的中点,所以|F1P|=2|OQ|=2b,
由椭圆的定义得|PF2|=2a-2b,由F1P⊥F2P,得(2b)2+(2a-2b)2=(2c)2,解得2a=3b,e=$\frac{\sqrt{5}}{3}$,
所以${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$=$\frac{1}{2}$(a+$\frac{5}{9a}$)≥$\frac{1}{2}$•2$\sqrt{a•\frac{5}{9a}}$=$\frac{\sqrt{5}}{3}$(当且仅当a=$\frac{\sqrt{5}}{3}$时等号成立).
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查最值的求法,注意运用椭圆的定义和基本不等式,考查圆的切线的性质的运用,以及中位线定理和勾股定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
1.在△ABC中,b=17,c=24,B=45°,则此三角形解的情况是( )
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |
11.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),直线l过不同的两点(a,0),($\frac{a+b}{2}$,$\frac{{ab-{b^2}}}{2a}$),若坐标原点到直线l的距离为$\frac{{\sqrt{3}c}}{4}$,则双曲线C的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | 2或$\frac{{2\sqrt{3}}}{3}$ |
18.某高中有甲乙两个班级进行数学考试,按照大于或等于90分为优秀,90分以下为非优秀统计成绩后,得到如下的列联表:
(1)请完成上面的列联表;
(2)根据列联表的数据,能否在犯错误的概率不超过0.05的前提下认为成绩与班级有关系?
参考公式:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}(其中n=a+b+c+d$为样本容量)
随机变量K2的概率分布:
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 55 |
| 合计 | 30 | 75 | 105 |
(2)根据列联表的数据,能否在犯错误的概率不超过0.05的前提下认为成绩与班级有关系?
参考公式:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}(其中n=a+b+c+d$为样本容量)
随机变量K2的概率分布:
| p(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15.函数y=b+asinx(a<0)的最大值为-1,最小值为-5,则y=tan(3a+b)x的最小正周期为( )
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |