题目内容
求sin410°+sin450°+sin470°的值为 .
考点:二倍角的余弦,同角三角函数基本关系的运用
专题:三角函数的求值
分析:原式各项利用诱导公式化简将正弦变形为余弦,利用二倍角的余弦函数公式化简,利用完全平方公式整理后,利用和差化积公式及诱导公式化简,计算即可得到结果.
解答:
解:sin410°+sin450°+sin470°
=cos480°+cos440°+cos420°
=cos420+cos440°+cos480°
=(
)2+(
)2+(
)2
=
+
(cos40°+cos80°+cos160°)+
(cos240°+cos280°+cos2160°)
=
+
(2cos60°cos20°-cos20°)+
(
+
+
)
=
+0+
(3+cos80°-cos20°+cos40°)
=
+
(3-2sin50°sin30°+sin50°)
=
+
=
.
故答案为:
=cos480°+cos440°+cos420°
=cos420+cos440°+cos480°
=(
| 1+cos40° |
| 2 |
| 1+cos80° |
| 2 |
| 1+cos160° |
| 2 |
=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1+cos80° |
| 2 |
| 1+cos160° |
| 2 |
| 1+cos320° |
| 2 |
=
| 3 |
| 4 |
| 1 |
| 8 |
=
| 3 |
| 4 |
| 1 |
| 8 |
=
| 3 |
| 4 |
| 3 |
| 8 |
=
| 9 |
| 8 |
故答案为:
| 9 |
| 8 |
点评:此题考查了同角三角函数基本关系的运用,二倍角的余弦函数公式,诱导公式,以及和差化积公式,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
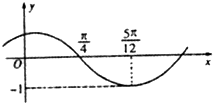 从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
设z1=i5+i6…+i12,z2=i5•i6…i12,则z1,z2的关系是( )
| A、z1=z2 |
| B、z1=-z2 |
| C、z1=z2-1 |
| D、无法确定 |