题目内容
等差数列{an},Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
| A、d<0 |
| B、S9>S5 |
| C、a7=0 |
| D、S6与S7是Sn的最大值 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:利用结论:n≥2时,an=sn-sn-1,结合题意易推出a6>0,a7=0,a8<0,然后逐一分析各选项.
解答:
解:设等差数列{an}的公差为d,
对于A、∵S5<S6=S7>S8,∴S6-S5=a6>0,S8-S7=a8<0,
即a6+2d<0,∴2d<-a6<0,∴d<0,即A正确;
对于B、S9-S5=a6+a7+a8+a9=2(a7+a8)=2(0+a8)=2a8<0,
∴S9<S5,故B错误;
对于C、S6=S7,∴S7-S6=a7=0,即C正确;
对于D、S5<S6=S7>S8,∴S6和S7均为Sn的最大值,即D正确,
故选:B.
对于A、∵S5<S6=S7>S8,∴S6-S5=a6>0,S8-S7=a8<0,
即a6+2d<0,∴2d<-a6<0,∴d<0,即A正确;
对于B、S9-S5=a6+a7+a8+a9=2(a7+a8)=2(0+a8)=2a8<0,
∴S9<S5,故B错误;
对于C、S6=S7,∴S7-S6=a7=0,即C正确;
对于D、S5<S6=S7>S8,∴S6和S7均为Sn的最大值,即D正确,
故选:B.
点评:本题考查了等差数列的前n项和公式、性质,以及sn的最值问题,熟练应用公式是解题的关键,注意等价转化思想的合理运用.

练习册系列答案
相关题目
“|x-a|<m,且|y-a|<m”是“|x-y|<2m”(x,y,a,m∈R)的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边.使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为( )米.
| A、1800 | B、2000 |
| C、2200 | D、2400 |
在△ABC中,a,b,c分别是内角A,B,C的对边,且cos2B+3cos(A+C)+2=0,b=
,则b:sinB的值是( )
| 3 |
| A、3:1 | ||
B、
| ||
C、
| ||
| D、2:1 |
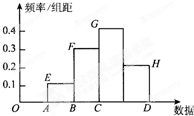 如图,已知样本容量为100,在样本频率分布直方图中,各小长方形的高的比是AE:BF:CG:DH=1:3:4:2,那么第3小组的频率与频数分别为( )
如图,已知样本容量为100,在样本频率分布直方图中,各小长方形的高的比是AE:BF:CG:DH=1:3:4:2,那么第3小组的频率与频数分别为( )| A、0.4,40 |
| B、0.3,30 |
| C、0.2,20 |
| D、0.1,10 |
已知数列:1、-1、1、-1、1、-1…,下列说法正确的是( )
| A、没有通项公式 |
| B、有一个通项公式 |
| C、有多种形式的通项公式 |
| D、以上说法不正确 |
直线L1:x+y+1=0,l2:ax-2y+4=0,若L1∥L2,则a等于( )
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
如图给出的是计算
+
+
+…+
的值的一个流程图,其中判断框内应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i>11 | B、i<10 |
| C、i≥10 | D、i>10 |