题目内容
2．为了考察某种药物预防禽流感的效果，某研究中心选了50只鸭子做实验，统计结果如下：| 得禽流感 | 不得禽流感 | 总计 | |
| 服药 | 5 | 20 | 25 |
| 不服药 | 15 | 10 | 25 |
| 总计 | 20 | 30 | 50 |
（2）在服药后得禽流感的鸭子中，有2只母鸭，3只公鸭，在这5只中随机抽取3只再进行研究，求至少抽到1只母鸭的概率．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
临界值表：
| P（K2≥k0） | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 （1）根据公式假设K2的值，对照临界值表即可得出结论；
（2）利用列举法求出基本事件数，计算所求的概率值．
解答 解：（1）假设H0：服药与家禽得流感没有关系，
则K2=$\frac{50{×（5×10-15×20）}^{2}}{20×30×25×25}$≈8.333＞6.635
∵P（K2＞6.635）=0.01，
1-0.01=0.99，
∴有99%的把握认为药物有效；
（2）记2只母鸭为a、b，3只公鸭为A、B、C，
则从这5只中随机抽取3只的基本事件为：
abA、abB、abC、aAB、aAC、aBC、bAB、bAC、bBC、ABC共10种，
则至少抽到1只母鸭的基本事件是9种，
故所求的概率为P=$\frac{9}{10}$．
点评 本题考查了独立性检验与列举法求古典概型的概率问题，是基础题目．
练习册系列答案
相关题目
12．若集合M={y|y=$\frac{1}{{x}^{2}}$}，N={x|y=$\sqrt{x-1}$}，那么M∩N=（ ）
| A． | （0，+∞） | B． | （1，+∞） | C． | [1，+∞） | D． | [0，+∞） |
13．已知曲线y=$\frac{{x}^{2}}{2}$-3lnx的一条切线的与直线x+2y+10=0垂直，则切点的横坐标为（ ）
| A． | $\frac{1}{3}$ | B． | 2 | C． | 1 | D． | 3 |
7．已知函数f（x）是定义域R在上的奇函数，且在区间[0，+∞）单调递增，若实数a满足f（log2a）+f（log2$\frac{1}{a}$）≤2f（1），则a的取值范围是（ ）
| A． | （-∞，2] | B． | $（{0，\frac{1}{2}}]$ | C． | $[{\frac{1}{2}，2}]$ | D． | （0，2] |
11．由1，2，3这三个数字组成的没有重复数字的三位自然数共有（ ）
| A． | 6个 | B． | 8个 | C． | 12个 | D． | 15个 |
12．
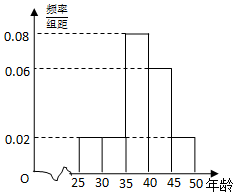某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图：
（1）如表是年龄的频数分布表，求a，b的值；
（2）根据频率分布直方图估计志愿者年龄的平均数和中位数；
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的分别抽取多少人？
（4）在（3）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图：（1）如表是年龄的频数分布表，求a，b的值；
| 区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
| 人数 | 50 | 50 | a | 150 | b |
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的分别抽取多少人？
（4）在（3）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．