题目内容
14. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=PB=6,M为PC上一点,满足2PM=MC.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=PB=6,M为PC上一点,满足2PM=MC.(1)若点N为AB边上的中点,试探究PN与平面BDM的位置关系,并说明理由;
(2)求三棱锥M-BDC的体积.
分析 (1)连结CN,交BD于E,连结ME,则△BEN∽△DEC,于是$\frac{CE}{CN}=\frac{2}{3}$.由2PM=MC得$\frac{CM}{PC}$=$\frac{2}{3}$.故而$\frac{CE}{CN}=\frac{CM}{PC}$,得到$\frac{CE}{CN}=\frac{CM}{PC}$,推出PN∥平面BDM.
(2)由PA=PD=AD=PB=AB=6,∠BAD=60°可得三棱锥P-ABD是棱长为6正四面体,求出P到底面的距离,根据$\frac{PM}{PC}=\frac{1}{3}$可得M到底面的距离,代入棱锥的体积公式计算即可.
解答  解(1)PN∥平面BDM.证明如下:
解(1)PN∥平面BDM.证明如下:
连结CN,交BD于E,连结ME,则△BEN∽△DEC,
∴$\frac{CE}{NE}=\frac{CD}{NB}=2$,∴$\frac{CE}{CN}=\frac{2}{3}$.
∵2PM=MC,∴$\frac{CM}{PC}$=$\frac{2}{3}$.
∴$\frac{CE}{CN}=\frac{CM}{PC}$,
∴PN∥ME,∵ME?平面BDM,PN?平面BDM,
∴PN∥平面BDM.
(2)过P做PF⊥平面ABCD,垂足为F,
∵PA=PD=AD=PB=AD=AB=6,∴F是△ABD的中心,
∴AF=2$\sqrt{3}$,∴PF=$\sqrt{P{A}^{2}-A{F}^{2}}$=2$\sqrt{6}$.
∴M到平面ABCD的距离d=$\frac{2}{3}$PF=$\frac{4\sqrt{6}}{3}$.
∴三棱锥M-BDC的体积V=$\frac{1}{3}$S△BCD•d=$\frac{1}{3}×\frac{1}{2}×6×6×sin60°$×$\frac{4\sqrt{6}}{3}$=12$\sqrt{2}$.
点评 本题考查了线面平行的判定,点到平面的距离计算,棱锥的体积计算,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $2\sqrt{2}$ | B. | $2\sqrt{2}+1$ | C. | $2\sqrt{2}+2$ | D. | $4\sqrt{2}+1$ |
 在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABC、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是( )
在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABC、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是( )| A. | 110 | B. | 116 | C. | 118 | D. | 120 |
| A. | {1,4} | B. | {1,3} | C. | {1,3,4} | D. | {0,1,3,4} |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.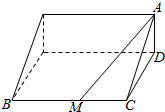 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.