题目内容
19.已知函数f(x)是定义在R上的奇函数,当x∈[0,1)时,f(x)=x,则$f({-\frac{1}{2}})$=$-\frac{1}{2}$.分析 根据函数奇偶性的性质进行转化求解即可.
解答 解:∵f(x)是定义在R上的奇函数,当x∈[0,1)时,f(x)=x,
∴$f({-\frac{1}{2}})$=-f($\frac{1}{2}$)=$-\frac{1}{2}$,
故答案为:$-\frac{1}{2}$
点评 本题主要考查函数值的计算,根据函数奇偶性的性质进行转化是解决本题的关键.比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.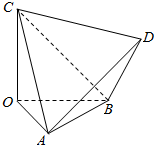 在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
 在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )| A. | OA,OB,OC的长度可以不相等 | B. | 直线OB∥平面ACD | ||
| C. | 直线OD与BC所成的角是45° | D. | 直线AD与OB所成的角是45° |
8.下列四个函数中,与y=x表示同一函数的而是( )
| A. | y=$\frac{{x}^{2}}{x}$ | B. | y=$\sqrt{{x}^{2}}$ | C. | y=($\sqrt{x}$)2 | D. | y=$\root{3}{{x}^{3}}$ |
9.已知直线l的方向向量为$\overrightarrow{a}$=(1,0,2),平面α的法向量$\overrightarrow{n}$=(-1,0,-2),则( )
| A. | l?α | B. | l⊥α | C. | l∥α | D. | l与α斜交 |
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=PB=6,M为PC上一点,满足2PM=MC.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=PB=6,M为PC上一点,满足2PM=MC.