题目内容
3.已知抛物线y=ax2+bx+c通过点P(1,1),且在点Q(2,-1)处的切线平行于直线y=x,则抛物线方程为( )| A. | y=3x2-11x+9 | B. | y=3x2+11x+9 | C. | y=3x2-11x-9 | D. | y=-3x2-11x+9 |
分析 先求导数y′=2ax+b,而根据条件知抛物线过点P(1,1),Q(2,-1),以及在Q点的切线斜率为1,这样便可得出关于a,b,c的方程组$\left\{\begin{array}{l}{a+b+c=1}\\{4a+2b+c=-1}\\{4a+b=1}\end{array}\right.$,解出a,b,c便可得出抛物线的方程.
解答 解:y′=2ax+b,抛物线在点Q(2,-1)处的切线斜率为:4a+b;
根据条件知抛物线过P,Q点,过Q的切线斜率为1;
$\left\{\begin{array}{l}{a+b+c=1}\\{4a+2b+c=-1}\\{4a+b=1}\end{array}\right.$;
解得$\left\{\begin{array}{l}{a=3}\\{b=-11}\\{c=9}\end{array}\right.$;
∴抛物线方程为y=3x2-11x+9.
故选:A.
点评 考查函数在某点的导数和过该点切线斜率的关系,以及平行直线的斜率关系,曲线上的点的坐标和曲线方程的关系.

练习册系列答案
相关题目
11.已知$\overrightarrow a=(5,6),\overrightarrow b=(sinα,cosα)$,且$\overrightarrow a∥\overrightarrow b$,则tanα=( )
| A. | $-\frac{5}{6}$ | B. | $-\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
15.函数f(x)=x2-2mx+5在区间[-2,+∞)上是增函数,则m的取值范围是( )
| A. | (-∞,-2] | B. | [-2,+∞) | C. | (-∞,-1] | D. | [-1,+∞) |
12.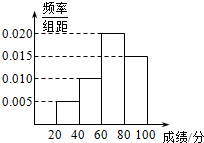 学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )
学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )
 学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )
学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )| A. | 45,67 | B. | 50,68 | C. | 55,69 | D. | 60,70 |
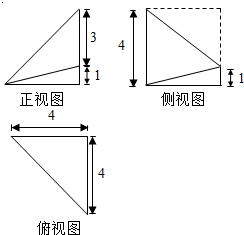 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.