题目内容
12.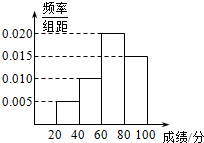 学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )
学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )| A. | 45,67 | B. | 50,68 | C. | 55,69 | D. | 60,70 |
分析 根据频率分布直方图,利用频率、频数与样本容量的关系,求出该班的学生数,再计算平均成绩.
解答 解:根据频率分布直方图,得;
低于60分的频率是(0.005+0.01)×20=0.3,
所以该班的学生人数为$\frac{15}{0.3}$=50,;
所以,该班的平均成绩为:
30×0.005×20+50×0.01×20+70×0.02×20+90×0.015×20=68.
故选:B.
点评 本题考查了频率分布直方图的应用问题,也考查了频率=$\frac{频数}{样本容量}$的应用问题,考查了求平均数的计算问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.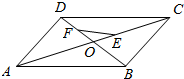 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )| A. | $\overrightarrow{FE}$=-$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | B. | $\overrightarrow{FE}$=$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | C. | $\overrightarrow{FE}$=$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ | D. | $\overrightarrow{FE}$=-$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ |
3.已知抛物线y=ax2+bx+c通过点P(1,1),且在点Q(2,-1)处的切线平行于直线y=x,则抛物线方程为( )
| A. | y=3x2-11x+9 | B. | y=3x2+11x+9 | C. | y=3x2-11x-9 | D. | y=-3x2-11x+9 |
17.以双曲线$\frac{x^2}{4}-{y^2}=1$的中心为顶点,右焦点为焦点的抛物线方程是( )
| A. | y2=4x | B. | ${y^2}=4\sqrt{5}x$ | C. | ${y^2}=8\sqrt{5}x$ | D. | ${y^2}=\sqrt{5}x$ |
1.圆C的方程为:x2+y2-6x-8y+23=0,则圆心C到点A(-1,1)的距离为( )
| A. | $\sqrt{13}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 5 |