题目内容
18.已知函数$f(x)=a{x^2}+blnx,a,b∈R,f(1)=\frac{1}{2},f'(2)=1$.(Ⅰ)求f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)在区间$[{1,\sqrt{e}}]$上的值域.
分析 (Ⅰ)求出函数的导数,由条件解方程可得a,b,求得切点和切线的斜率,由点斜式方程可得切线的方程;
(Ⅱ)求出函数的导数,求得f(x)在区间$[{1,\sqrt{e}}]$上的单调区间,可得极小值也为最小值,求得端点处的函数值,可得最大值,即可得到函数的值域.
解答 解:(Ⅰ)f(x)=ax2+blnx的导数为f′(x)=2ax+$\frac{b}{x}$,
由f(1)=$\frac{1}{2}$,f′(2)=1,可得a=$\frac{1}{2}$,4a+$\frac{b}{2}$=1,
解方程可得b=-2,即有f(x)=$\frac{1}{2}$x2-2lnx,f′(1)=-1,
则在点(1,f(1))处的切线方程为y-$\frac{1}{2}$=-(x-1),
即为2x+2y-3=0;
(Ⅱ)f(x)的导数为f′(x)=x-$\frac{2}{x}$=$\frac{(x-\sqrt{2})(x+\sqrt{2})}{x}$,
当1<x<$\sqrt{2}$时,f′(x)<0,f(x)递减;
当$\sqrt{2}$<x<$\sqrt{e}$时,f′(x)>0,f(x)递增.
即有f(x)在x=$\sqrt{2}$处取得极小值,也为最小值,且为1-ln2;
f(1)=$\frac{1}{2}$,f($\sqrt{e}$)=$\frac{1}{2}$e-1,
由f($\sqrt{e}$)-f(1)=$\frac{e-3}{2}$<0,即有f($\sqrt{e}$)<f(1),
则f(x)的值域为[1-ln2,$\frac{1}{2}$].
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查运算能力,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
8.已知函数f(x)=2|x+1|+ax(x∈R),若函数f(x)存在两个零点,则a的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | [0,2) | D. | [0,2] |
13.设变量x,y满足约束条件$\left\{\begin{array}{l}2x+y≤4\\ x+2y≥2\\ x≥0\end{array}\right.$,则目标函数z=x-y的最小值为( )
| A. | 2 | B. | -4 | C. | -1 | D. | 4 |
3.已知抛物线y=ax2+bx+c通过点P(1,1),且在点Q(2,-1)处的切线平行于直线y=x,则抛物线方程为( )
| A. | y=3x2-11x+9 | B. | y=3x2+11x+9 | C. | y=3x2-11x-9 | D. | y=-3x2-11x+9 |
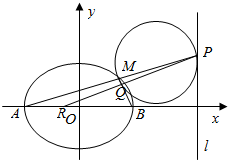 如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.
如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.