题目内容
把“五进制”数234（5）转化为“十进制”数，再把它转化为“二进制”数．
考点：进位制
专题：计算题
分析：首先把五进制数字转化成十进制数字，用所给的数字最后一个数乘以5的0次方，依次向前类推，相加得到十进制数字，再用这个数字除以2，倒序取余即可．．
解答：
解：234（5）=2×52+3×51+4×50=69（10）
69÷2=34…1
34÷2=17…0
17÷2=8…1
8÷2=4…0
4÷2=2…0
2÷2=1…0
1÷2=0…1
故：69（10）=1000101 （2）
故：234（5）=69（10）=1000101（2）（10分）
69÷2=34…1
34÷2=17…0
17÷2=8…1
8÷2=4…0
4÷2=2…0
2÷2=1…0
1÷2=0…1
故：69（10）=1000101 （2）
故：234（5）=69（10）=1000101（2）（10分）
点评：本题考查进位制之间的转化，本题涉及到三个进位制之间的转化，实际上不管是什么之间的转化，原理都是相同的，属于基础题．
练习册系列答案
相关题目
已知集合A={x|x2-2x-3=0}，B={x|x2+x-12＜0}，则A∩B等于（ ）
| A、{-1} | B、{-3} |
| C、{1} |
已知命题p：x2+2x-3＞0；命题q：x＞a，且?q的一个充分不必要条件是?p，则实数a的取值范围是（ ）
| A、（-∞，1] |
| B、（-∞，-3] |
| C、[-1，+∞） |
| D、[1，+∞） |
函数f（x）=xsinx2在区间[0，4]上的零点个数为（ ）
| A、4 | B、5 | C、6 | D、7 |
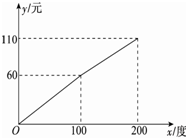某供电公司为了合理分配电力，采用分段计算电费政策，月用电量x（度）与相应电费y（元）之间的函数关系的图象如图所示．
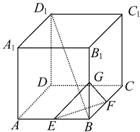在棱长为1的正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹的长度为（ ）