题目内容
4.(1-$\root{3}{x}$)8展开式中x的系数为-56.分析 在二项展开式的通项公式中,令x的幂指数等于1,求出r的值,即可求得x的系数.
解答 解:由于(1-$\root{3}{x}$)8展开式的通项公式为Tr+1=${C}_{8}^{r}$•(-1)r•${x}^{\frac{r}{3}}$,令$\frac{r}{3}$=1,可得r=3,
故展开式中x的系数为-56,
故答案为:-56.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下面的命题中是真命题的是( )
| A. | 两个平面的法向量所成的角是这两个平面所成的角 | |
| B. | 设空间向量$\overrightarrow a$,$\overrightarrow b$为非零向量,若$\overrightarrow a•\overrightarrow b>0$,则$<\overrightarrow a,\overrightarrow b>$为锐角 | |
| C. | 方程mx2+ny2=1(m>0,n>0)表示的曲线是椭圆 | |
| D. | 等轴双曲线的渐近线互相垂直,离心率等于$\sqrt{2}$ |
14.△ABC的内角A,B,C的对边分别为a,b,c,满足$\frac{a-b+c}{b}≤\frac{c}{a+b-c}$,则角A的范围是( )
| A. | $({0,\frac{π}{6}}]$ | B. | $({0,\frac{π}{3}}]$ | C. | $[{\frac{π}{6},π})$ | D. | $[{\frac{π}{3},π})$ |
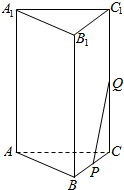 如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.
如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20. 过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C两点.若PA=6,AC=4,BC=9,求AB的值.
过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C两点.若PA=6,AC=4,BC=9,求AB的值.