题目内容
“函数f(x)=cos2ax-sin2ax的最小正周期为2π”是“a=-
”的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据三角函数的性质和周期公式,利用充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:∵f(x)=cos2ax-sin2ax=cos2ax,
∴若函数的周期是2π,即T=
=2π,
即a=±
,∴充分性不成立.
若a=-
,则函数的周期T=
=2π,∴必要性成立.
即“函数f(x)=cos2ax-sin2ax的最小正周期为2π”是“a=-
”的成立的必要不充分条件.
故选:B
∴若函数的周期是2π,即T=
| 2π |
| |2a| |
即a=±
| 1 |
| 2 |
若a=-
| 1 |
| 2 |
| 2π |
| |2a| |
即“函数f(x)=cos2ax-sin2ax的最小正周期为2π”是“a=-
| 1 |
| 2 |
故选:B
点评:本题主要考查充分条件和必要条件的判断,利用三角函数的图象和性质是解决的关键,比较基础.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
如图是某算法的程序框图,则程序运行后输出的结果是( )

| A、8 | B、9 | C、10 | D、11 |
等差数列{an}满足an∈N*,且前10项和S10=280,则a9最大值是( )
| A、28 | B、49 | C、50 | D、52 |
已知命题p:?φ∈R,使f(x)=sin(x+φ)为偶函数;命题q:?x∈R,cos2x+4sinx-3<0,则下列命题中为真命题的是( )
| A、p∧q |
| B、(¬p)∨q |
| C、p∨(¬q) |
| D、(¬p)∧(¬q) |
一个扇形的弧长与面积都是5,则这个扇形圆心角的弧度数为( )
| A、2rad | ||
B、
| ||
| C、1rad | ||
D、
|
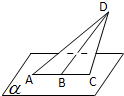 平面ACD⊥平面α,B为AC的中点,AC=2,∠CBD=60°,P是α内的动点,且P到直线BD的距离为
平面ACD⊥平面α,B为AC的中点,AC=2,∠CBD=60°,P是α内的动点,且P到直线BD的距离为 某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )


