题目内容
(1)若α是第二象限角,sin(π-α)=
.求
的值;
(2)已知函数f(x)=tan(2x+
),设α∈(0,
),若f(
)=2cos2α,求α的大小.
| ||
| 10 |
2sin2
| ||||||||
|
(2)已知函数f(x)=tan(2x+
| π |
| 4 |
| π |
| 4 |
| α |
| 2 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)利用诱导公式求出sinα,通过二倍角公式化简所求表达式,然后求解即可.
(2)利用函数的解析式通过弦切互化,二倍角的余弦函数,结合角的范围,求出cosα-sinα=
,然后求解角的大小.
(2)利用函数的解析式通过弦切互化,二倍角的余弦函数,结合角的范围,求出cosα-sinα=
| ||
| 2 |
解答:
解:(1)sin(π-α)=
.sinα=
.α是第二象限角,∴cosα=-
.
=
=
=
-
.
(2)函数f(x)=tan(2x+
),若f(
)=2cos2α,可得:tan(α+
)=2cos2α,
可得
=2(cosα-sinα)(cosα+sinα),α∈(0,
),可得cosα-sinα=
,
1-sin2α=
,∴sin2α=
,α∈(0,
),∴2α=
,
∴α=
.
| ||
| 10 |
| ||
| 10 |
3
| ||
| 10 |
2sin2
| ||||||||
|
8sin
| ||||||
| sinα-cosα |
| 4sinα+3cosα |
| sinα-cosα |
4×
| ||||||||
|
| 5 |
| 4 |
(2)函数f(x)=tan(2x+
| π |
| 4 |
| α |
| 2 |
| π |
| 4 |
可得
| cosα+sinα |
| cosα-sinα |
| π |
| 4 |
| ||
| 2 |
1-sin2α=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 6 |
∴α=
| π |
| 12 |
点评:本题考查三角函数的化简求值,弦切互化,二倍角公式以及同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
若复数z满足(1-3i)z=10i,则z等于( )
| A、-1-3i | B、3-i |
| C、1+3i | D、-3+i |
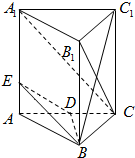 已知三棱柱ABC-A1B1C1中,AB=2,AA1=
已知三棱柱ABC-A1B1C1中,AB=2,AA1=| 3 |
(Ⅰ)当E为AA1中点时,求证:ED∥平面A1B2C
(Ⅱ)当点A到平面BDE的距离为
| 1 |
| 2 |
经过点A(-4,3)且与原点的距离等于5的直线方程是( )
| A、3x-4y+25=0 |
| B、4x-3y-25=0 |
| C、4x-3y+25=0 |
| D、4x+3y+25=0 |
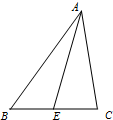 如图,在△ABC中,∠BAC=
如图,在△ABC中,∠BAC=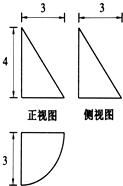 某几何体的三视图(单位:cm)如图所示,其中俯视图中的曲线是四分之一的圆弧,则该几何体的体积等于
某几何体的三视图(单位:cm)如图所示,其中俯视图中的曲线是四分之一的圆弧,则该几何体的体积等于