题目内容
函数f（x）=
，则关于x的方程f（x）-x=0的解的个数是（ ）
|
| A、4 | B、3 | C、2 | D、1 |
考点：根的存在性及根的个数判断
专题：计算题,作图题,函数的性质及应用
分析：关于x的方程f（x）-x=0的解的个数即函数f（x）=
的图象与y=x的交点的个数，作图求解．
|
解答：
解：关于x的方程f（x）-x=0的解的个数即
函数f（x）=
的图象与y=x的交点的个数，
作函数f（x）=
与y=x的图象可得，
由图可知有两个交点，
故关于x的方程f（x）-x=0的解的个数是2；
故选C．
函数f（x）=
|
作函数f（x）=
|
由图可知有两个交点，
故关于x的方程f（x）-x=0的解的个数是2；
故选C．
点评：本题考查了学生的作图能力及方程的根与函数的图象的关系，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的偶函数满足f（x）满足f（x）=-
，当x∈[3，4]时，f（x）=x-2，则（ ）
| 1 |
| f(x-1) |
| A、f（sin2）＞f（cos2） | ||||
B、f（sin
| ||||
| C、f（sin1）＞f（cos1） | ||||
D、f（sin
|
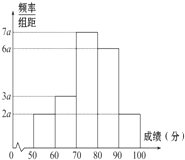从100名学生中抽取20名学生某次数学考试成绩（单位：分）的频率分布直方图如下：