Question

线段AB与CD互相垂直平分于点O，|

AB

|=2a，|

CD

|=2b，动点P满足|

PA

|•|

PB

|=|

PC

|•|

PD

|，则动点P的轨迹方程为

 

．

Answer 1

考点：轨迹方程

专题：圆锥曲线的定义、性质与方程

分析：以AB中点O为原点，直线AB所在直线为x轴，CD所在直线为y轴，建立直角坐标系，设P（x，y），由题设知

(x+a)2+y2

•

(x-a)2+y2

=

x2+(y+b)2

•

x2+(y-b)2

．由此能求出动点P的轨迹方程．

解答： 解：以AB中点O为原点，直线AB所在直线为x轴，CD所在直线为y轴，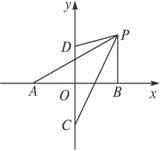
建立如图所示的直角坐标系，
设P（x，y），又A（-a，0），B（a，0），C（0，-b），D（0，b）．由题设知|

PA

|•|

PB

|=|

PC

|•|

PD

|，
∴

(x+a)2+y2

•

(x-a)2+y2

=

x2+(y+b)2

•

x2+(y-b)2

．
化简，得x²-y²=

a2-b2

2

．
故答案为：x²-y²=

a2-b2

2

．

点评：本题考查动点的轨迹方程的求法，是中档题，解题时要认真审题，注意两点间距离公式的合理运用．