题目内容
14.已知圆C:(x-1)2+y2=r2(r>0)与直线l:y=x+3,且直线l上有唯一的一个点P,使得过点P作圆C的两条切线互相垂直.设EF是直线l上的一条线段,若对于圆C上的任意一点Q,$\overrightarrow{QE}•\overrightarrow{QF}≤0$,则$|{\overrightarrow{EF}}|$的最小值是4+4$\sqrt{2}$.分析 由圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,求得PC所在直线方程,与直线l求得交点P,再根据对称性可得r=2,由题意,知|EF|取得最小值时,一定关于直线y=-x+1对称,画出图形,通过图形观察,当两圆相内切时,求得最小值.
解答 解:根据圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,
则PC所在直线的方程为x+y=1,与直线y=x+3联立求得P(-1,2),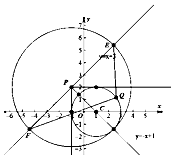
再根据对称性知过点P(-1,2)的两条切线必与坐标轴垂直,r=2;
由题意,知|EF|取得最小值时,一定关于直线y=-x+1对称,如图所示,
因此可设以点P(-1,2)为圆心,以R为半径的圆,
即(x+1)2+(y-2)2=R2与圆C内切时,
$|{\overrightarrow{EF}}|$的最小值即为2R,
由相切条件易知2R=2(|CP|+2)=2(2$\sqrt{2}$+2)=4+4$\sqrt{2}$.
故答案为:4+4$\sqrt{2}$.
点评 本题考查直线和圆的位置关系,圆与圆的位置关系,考查数形结合思想方法,注意几何法的运用,考查运算能力,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5.已知函数f(x)=ax3+bx(a,b∈R)的图象如图所示,则a,b的关系是( )


| A. | 3a-b=0 | B. | 3a+b=0 | C. | a-3b=0 | D. | a+3b=0 |
9.市教育局为了对学校教学水平和学校管理水平评价,从某校学生中选出200人进行统计,其中对学校教学水平给出好评的学生人数为总数的60%,对学校管理水平给出好评的学生人数为总数的75%,其中对学校教学水平和学校管理水平给出好评的有80人.
(1)填写学校教学水平和学校管理水平评价的2×2列联表:
(2)问:是否可以在犯错误概率不超过0.1%的前提下,认为学校的教学水平好评与学校管理水平好评有关?
$({{k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}})$其中n=a+b+c+d.
| 对学校管理水平好评 | 对学校管理水平不满意 | 合计 | |
| 对学校教学水平好评 | |||
| 对学校教学水平不满意 | |||
| 合计 |
(2)问:是否可以在犯错误概率不超过0.1%的前提下,认为学校的教学水平好评与学校管理水平好评有关?
| p(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.圆x2+y2+2ax+4ay=0的半径为$\sqrt{5}$,则a等于( )
| A. | 5 | B. | -5或5 | C. | 1 | D. | 1或-1 |
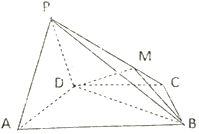 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.