题目内容
已知椭圆C:4x2+y2=1及直线l:y=x+m,m∈R.
(1)求直线l被椭圆C截得的弦的中点的轨迹;
(2)若直线l交椭圆C于P、Q两点,且OP⊥OQ,求直线l的方程.
(1)求直线l被椭圆C截得的弦的中点的轨迹;
(2)若直线l交椭圆C于P、Q两点,且OP⊥OQ,求直线l的方程.
考点:椭圆的简单性质,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:对于第(1)问,设l与C交于A(x1,y1),B(x2,y2),弦AB的中点为M(x0,y0),联立椭圆C及直线l的方程,消去y,得到关于x的一元二次方程,由韦达定理及中点公式,可用m表示x0,根据中点M在直线l上,得y0,由x0与y0的表达式,消去m,得x0与y0的关系式,最后由△>0,得m的范围,从而得x0的范围,即可知弦AB的中点的轨迹.
对于第(2)问,设P(x3,y3),Q(x4,y4),联立椭圆C及直线l的方程,消去y,得到关于x的一元二次方程,由韦达定理,得x3+x4及x3x4,将x3,x4分别代入直线l的方程中,得y3y4,由OP⊥OQ,得
•
=0,将x3x4及y3y4代入,得到关于m的方程,解些方程并检验m的值即可.
对于第(2)问,设P(x3,y3),Q(x4,y4),联立椭圆C及直线l的方程,消去y,得到关于x的一元二次方程,由韦达定理,得x3+x4及x3x4,将x3,x4分别代入直线l的方程中,得y3y4,由OP⊥OQ,得
| OP |
| OQ |
解答:
解:(1)设l与C交于A(x1,y1),B(x2,y2),弦AB的中点为M(x0,y0).
由
,消去y,整理得5m2+2mx+m2-1=0,
因为直线l与椭圆C有两个交点,所以△>0,即(2m)2-4×5(m2-1)>0,得-
<m<
.…①
由韦达定理,得x1+x2=-
,即x0=
=-
m,…②
从而y0=-
m+m=
m,…③
由②、③,消去m,得y0=-4x0,
由①、②,得-
<x0<
,
得弦AB的中点M的轨迹为直线上y=-4x上满足-
<x<
的一条线段.
所以弦AB的中点M的轨迹为
(2)设P(x3,y3),Q(x4,y4),
由(1)知,x3+x4=-
,x3x4=
,
从而y3y4=(x3+m)(x4+m)=x3x4+m(x3+x4)+m2=
+m•(-
)+m2=
,
由OP⊥OQ,得
•
=0,
所以x3x4+y3y4=0,即
+
=0,
得m=±
,经检验,m=±
均符合题意,
故直线l的方程为y=x+
,或y=x-
.
由
|
因为直线l与椭圆C有两个交点,所以△>0,即(2m)2-4×5(m2-1)>0,得-
| ||
| 2 |
| ||
| 2 |
由韦达定理,得x1+x2=-
| 2m |
| 5 |
| x1+x2 |
| 2 |
| 1 |
| 5 |
从而y0=-
| 1 |
| 5 |
| 4 |
| 5 |
由②、③,消去m,得y0=-4x0,
由①、②,得-
| ||
| 10 |
| ||
| 10 |
得弦AB的中点M的轨迹为直线上y=-4x上满足-
| ||
| 10 |
| ||
| 10 |
所以弦AB的中点M的轨迹为
(2)设P(x3,y3),Q(x4,y4),
由(1)知,x3+x4=-
| 2m |
| 5 |
| m2-1 |
| 5 |
从而y3y4=(x3+m)(x4+m)=x3x4+m(x3+x4)+m2=
| m2-1 |
| 5 |
| 2m |
| 5 |
| 4m2-1 |
| 5 |
由OP⊥OQ,得
| OP |
| OQ |
所以x3x4+y3y4=0,即
| m2-1 |
| 5 |
| 4m2-1 |
| 5 |
得m=±
| ||
| 5 |
| ||
| 5 |
故直线l的方程为y=x+
| ||
| 5 |
| ||
| 5 |
点评:本题考查了直线与椭圆相交的关系、轨迹问题、中点弦及垂直问题,关键是利用韦达定理及直线方程进行转换.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知点A(-1,2),B(1,3),若直线l与直线AB平行,则直线l的斜率为( )
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
若复数z1=5+13i,z2=7+28i,其中i是虚数单位,则复数(z1-z2)i的实部为 (
| A、-20 | B、15 | C、30 | D、8 |
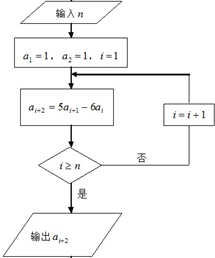 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图.