题目内容
17.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,则( )| A. | f(-3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(-3) | C. | f(-2)<f(1)<f(-3) | D. | f(-3)<f(1)<f(-2) |
分析 先根据条件判断函数在(-∞,0]上单调递减,且函数为偶函数,进而得出f(1)<f(2)<f(3),再参考选项即可.
解答 解:因为,对任意的x1,x2∈(-∞,0],都有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,
所以,f(x)在区间(-∞,0]上单调递减,
又∵f(x)为偶函数,
∴f(x)的图象关于y轴对称,
因此,f(x)在[0,+∞)上单调递增,
所以,f(1)<f(2)<f(3),
而f(-3)=f(3),f(-2)=f(2),
所以,f(1)<f(-2)<f(-3),
故答案为:B.
点评 本题主要考查了函数单调性和奇偶性的综合应用,涉及单调性的判断和偶函数的性质,体现了数形结合的解题思想,属于中档题.

练习册系列答案
相关题目
8.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )
| A. | (1,$\sqrt{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,3] |
5.已知双曲线x${\;}^{2}-\frac{{y}^{2}}{{b}^{2}}=1$(b>0),若右焦点F(c,0)到一条渐近线的距离为2,则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
12.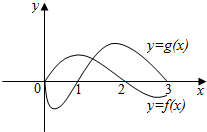 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
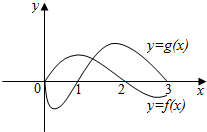 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )| A. | (0,1)∪(2,3) | B. | (-2,-1)∪(0,1)∪(2,3) | ||
| C. | (-1,0)∪(-3,-2)∪(0,1)∪(2,3) | D. | (-3,-1)∪(0,1)∪(2,3) |
7.已知圆C:(x+m)2+y2=4上存在两点关于直线x-y+3=0对称,则实数m的值是( )
| A. | -3 | B. | 6 | C. | 3 | D. | 无法确定 |
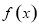 在
在 上存在导数
上存在导数 ,且在
,且在 上
上 ,若
,若 ,则实数
,则实数 的取值范围为( )
的取值范围为( ) B.
B.
 D.
D.