题目内容
12.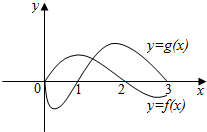 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )| A. | (0,1)∪(2,3) | B. | (-2,-1)∪(0,1)∪(2,3) | ||
| C. | (-1,0)∪(-3,-2)∪(0,1)∪(2,3) | D. | (-3,-1)∪(0,1)∪(2,3) |
分析 根据函数奇偶性的性质,分别求出不等式对应的解集,进行分类讨论进行求解即可.
解答 解:∵y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],
∴由图象知,f(x)>0得解集为(0,2)∪(-2,0),f(x)<0得解集为[-3,-2)∪[(2,3],
g(x)>0得解集为(-1,0)∪(1,3),g(x)<0得解集为(-3,-1)∪(0,1),
若f(x)•g(x)<0,
则$\left\{\begin{array}{l}{f(x)>0}\\{g(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{f(x)<0}\\{g(x)>0}\end{array}\right.$,
即g$\left\{\begin{array}{l}{0<x<2或-2<x<0}\\{-3<x<-1或0<x<1}\end{array}\right.$或$\left\{\begin{array}{l}{-3≤x<-2或2<x≤3}\\{-1<x<0或1<x<3}\end{array}\right.$,
即0<x<1或-2<x<-1或2<x<3,
即不等式f(x)•g(x)<0的解集为(-2,-1)∪(0,1)∪(2,3),
故选:B
点评 本题主要考查不等式的求解,根据函数奇偶性的性质以及数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.函数f(x)=-$\frac{1}{2}{x^3}$-sinx-2x的定义域为R,数列{an}是公差为d的等差数列,且a1+a2+a3+a4+…+a2015<0,记m=f(a1)+f(a2)+f(a3)+…+f(a2015),关于实数m,下列说法正确的是( )
| A. | m恒为负数 | |
| B. | 当d>0时,m恒为正数;当d<0时,m恒为负数 | |
| C. | m恒为正数 | |
| D. | 当d>0时,m恒为负数;当d<0时,m恒为正数 |
17.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,则( )
| A. | f(-3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(-3) | C. | f(-2)<f(1)<f(-3) | D. | f(-3)<f(1)<f(-2) |
 的前
的前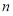 项和为
项和为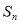 ,
,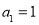 ,且
,且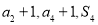 成等比数列.
成等比数列.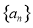 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 .
. 如图,四棱锥C-ABED中,四边形ABED是正方形,若G,F分别是线段EC,BD的中点.
如图,四棱锥C-ABED中,四边形ABED是正方形,若G,F分别是线段EC,BD的中点.