题目内容
已知抛物线方程y2=8x,直线L的方程为
x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线L的距离为d2,则d1+d2的最小值( )
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、
|
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:连接PF,过点P作PA⊥l于点A,作PB⊥y轴于点B,PB的延长线交准线x=-2于点C.由抛物线的定义,得到d1+d2=(PA+PF)-2,再由平面几何知识可得当P、A、F三点共线时,PA+PF有最小值,因此算出F到直线l的距离,即可得到d1+d2的最小值.
解答:
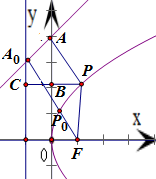 解:如图,过点P作PA⊥l于点A,作PB⊥y轴于点B,PB的延长线交准线x=-2于点C,
解:如图,过点P作PA⊥l于点A,作PB⊥y轴于点B,PB的延长线交准线x=-2于点C,
连接PF,根据抛物线的定义得PA+PC=PA+PF,
∵P到y轴的距离为d1,P到直线l的距离为d2,
∴d1+d2=PA+PB=(PA+PC)-2=(PA+PF)-2,
根据平面几何知识,可得当P、A、F三点共线时,PA+PF有最小值
∵F(2,0)到直线l:
x-y+4=0的距离为
=
+2,
∴PA+PF的最小值是
+2,
由此可得d1+d2的最小值为
+2-2=
.
故选:D.
 解:如图,过点P作PA⊥l于点A,作PB⊥y轴于点B,PB的延长线交准线x=-2于点C,
解:如图,过点P作PA⊥l于点A,作PB⊥y轴于点B,PB的延长线交准线x=-2于点C,连接PF,根据抛物线的定义得PA+PC=PA+PF,
∵P到y轴的距离为d1,P到直线l的距离为d2,
∴d1+d2=PA+PB=(PA+PC)-2=(PA+PF)-2,
根据平面几何知识,可得当P、A、F三点共线时,PA+PF有最小值
∵F(2,0)到直线l:
| 3 |
2
| ||
| 2 |
| 3 |
∴PA+PF的最小值是
| 3 |
由此可得d1+d2的最小值为
| 3 |
| 3 |
故选:D.
点评:本题给出抛物线和直线l,求抛物线上一点P到y轴距离与直线l距离之和的最小值,着重考查了点到直线的距离公式、抛物线的定义和简单几何性质等知识,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若sina=
,a是第二象限的角,则cosa=( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
设a,b∈R,则“a3<b3”是“a<b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
使函数f(x)=
在(-∞,+∞)上是减函数的一个充分不必要条件是( )
|
A、
| ||||
B、0<a<
| ||||
C、
| ||||
D、0<a<
|
若三个互不相等的正数x1,x2,x3满足方程xi+lnxi=mi(i=1,2,3),且m1+m3=2m2,则下列关系式正确的是( )
| A、x1x3<x22 |
| B、x1x3≤x22 |
| C、x1x3>x22 |
| D、x1x3≥x22 |
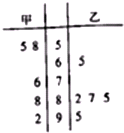 如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为
如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|