题目内容
2．函数f（x）=$\frac{cosx}{x}$的图象大致是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 利用函数的奇偶性排除选项，然后利用函数的变化趋势，判断选项即可．
解答 解：函数f（x）=$\frac{cosx}{x}$是奇函数，排除A，C，
当x＞0，并且x→0时，f（x）=$\frac{cosx}{x}$＞0，
排除D．
故选：B．
点评 本题考查函数的图象的判断，函数的奇偶性以及函数经过的特殊点是常用判断方法．
练习册系列答案
学习实践园地系列答案
相关题目
13．双曲线mx2+ny2=1（mn＜0）的一条渐近线方程为$y=\sqrt{3}x$，则它的离心率为（ ）
| A． | 2 | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\sqrt{3}$或$\frac{{2\sqrt{3}}}{3}$ | D． | 2或$\frac{{2\sqrt{3}}}{3}$ |
10．圆E经过三点A（0，1），B（2，0），C（0，-1），且圆心在x轴的正半轴上，则圆E的标准方程为（ ）
| A． | （x-$\frac{3}{2}$）2+y2=$\frac{25}{4}$ | B． | （x+$\frac{3}{4}$）2+y2=$\frac{25}{16}$ | C． | （x-$\frac{3}{4}$）2+y2=$\frac{25}{16}$ | D． | （x-$\frac{3}{4}$）2+y2=$\frac{25}{4}$ |
17．已知集合A={x|x≥3或x≤1}，B={x|x2-6x+8＜0}，则（∁RA）∩B=（ ）
| A． | （1，3） | B． | （1，4） | C． | （2，3） | D． | （2，4） |
7．
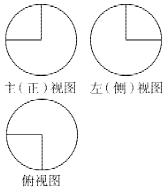如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径，若该几何体的表面积是17π，则它的体积是（ ）
如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径，若该几何体的表面积是17π，则它的体积是（ ）| A． | 8π | B． | $\frac{56π}{3}$ | C． | $\frac{14π}{3}$ | D． | $\frac{28π}{3}$ |
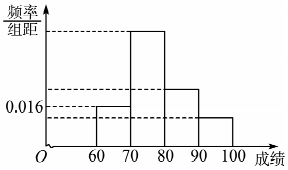某班为了提高学生学习英语的兴趣，在班内举行英语写、说、唱综合能力比赛，比赛分为预赛和决赛2个阶段，预赛为笔试，决赛为说英语、唱英语歌曲，将所有参加笔试的同学进行统计，得到频率分布直方图，其中后三个矩形高度之比依次为4：2：1，落在[80，90）的人数为12人．