题目内容
已知集合M={1,2,3,5},N={x|x=2k-1,k∈M},则M∩N=( )
| A、{1,2,3} |
| B、{1,3,5} |
| C、{2,3,5} |
| D、M |
考点:交集及其运算
专题:集合
分析:将M中元素代入x=2k-1计算确定出N,求出M与N的交集即可.
解答:
解:将k=1代入得:x=2k-1=1;
将k=2代入得:x=2k-1=3;
将k=3代入得:x=2k-1=5;
将k=5代入得:x=2k-1=9,
∴N={1,3,5,9},
∵M={1,2,3,5},
∴M∩N={1,3,5}.
故选:B.
将k=2代入得:x=2k-1=3;
将k=3代入得:x=2k-1=5;
将k=5代入得:x=2k-1=9,
∴N={1,3,5,9},
∵M={1,2,3,5},
∴M∩N={1,3,5}.
故选:B.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中,若a2-b2=
bc,sinC=2
sinB,则A=( )
| 3 |
| 3 |
| A、150° | B、60° |
| C、120° | D、30° |
设m∈R,若x>0时,均有[(m-1)x-1](x2-mx-1)≥0恒成立,则m=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个简单几何体的正视图、俯视图如图所示,则其侧视图不可能是( )
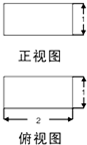

| A、正方形 | B、直角梯形 |
| C、等腰三角形 | D、圆 |
已知{an}为等差数列,{bn}为等比数列,其公比q≠1且bi>0(i=1,2,…,n),若a1=b1,a11=b11,则( )
| A、a6>b6 |
| B、a6=b6 |
| C、a6<b6 |
| D、a6≥b6 |
在复平面内,复数
+(1+i)2对应的点位于( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
满足a∈A且4-a∈A,a∈N且4-a∈N,有且只有2个元素的集合A的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |