题目内容

在△ABC中，若a：b：c=5：7：8，则∠B的大小是
 
．
考点：余弦定理
专题：解三角形
分析：根据a：b：c=5：7：8，设a=5k，b=7k，c=8k，代入余弦定理中求得cosB的值，进而求得B．
解答： 解：∵a：b：c=5：7：8
设a=5k，b=7k，c=8k，
由余弦定理可得cosB=
a2+c2-b2
2ac
=
1
2
；
∴∠B=
π
3
．
故答案为
π
3
．
点评：本题主要考查了余弦定理和正弦定理的应用．作为解三角形中常用的公式，应熟练掌握正弦定理和余弦定理及其变形公式．
练习册系列答案
相关题目
写出函数f（x）=-x2+2x-3的单调递增区间，并证明．
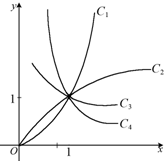如图是幂函数y=xn在第一象限内的图象，已知n取
1
2
，2，-2，-
1
2
四值，则相应于曲线C1，C2，C3，C4的n依次为（　　）
A、2，
1
2
，-
1
2
，-2
B、-2，-
1
2
，
1
2
，2
C、-
1
2
，-2，2，
1
2
D、2，
1
2
，-2，-
1
2
已知集合A={x|x＜2
3
}，a=2，则下列关系正确的是（　　）
A、a?AB、{a}∈A
C、a∈AD、a∉A
若a=0.32，b=20.3，c=log0.32，则a，b，c由大到小的关系是（　　）
A、a＞b＞c
B、b＞a＞c
C、b＞c＞a
D、c＞a＞b
已知2+ai，b+i（其中a，b∈R）是实系数一元二次方程x2+px+q=0的两个根，则
a+bi
p+qi
的值为
 
．
已知函数f（x）=loga
1+x
1-x
（a＞0，且 a≠1），则（　　）
A、f（x）是R上的奇函数
B、f（x）是R上的偶函数
C、f（x）在定义域上是奇函数
D、以上均不正确
下列各图中，表示以x为自变量的函数的图象是（　　）
A、
B、
C、
D、
等比数列{an}中，若a3a5a7=(-
3
)3，则a2a8=（　　）
A、3B、-3C、9D、-9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网