题目内容
12.高三某班要安排6名同学值日(周日休息),每天安排一人,每人值日一天,要求甲必须安排在周一到周四的某一天,乙必须安排在周五或周六的某一天,则不同的值日生表有多少种?( )| A. | 144 | B. | 192 | C. | 360 | D. | 720 |
分析 根据题意,分3步进行,先安排甲,再安排乙,最后安排其他的4人;依次求出其可能的情况数目,进而由分步计数原理,计算可得答案.
解答 解:根据题意,先安排甲,甲必须安排在周一到周四的某一天,有4种情况,
再安排乙,学乙必须安排在周五或周六的某一天,则乙有2种情况,
最后对其他的4人分析,将其安排在剩余的4天即可,有A44=24种情况,
由分步计数原理,可得共有4×2×24=192种情况,
故选B.
点评 本题考查排列、组合的综合应用,注意分步讨论时,优先分析受到限制的元素,本题先分析甲,再分析乙.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.空间直角坐标系中,点A(1,0,1)关于x轴对称的点为A',点B(2,1,-1),则$\frac{{|{AB}|}}{{|{A'B}|}}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | 3 | D. | $\sqrt{3}$ |
1.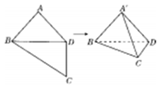 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )| A. | A'C⊥BD | B. | 四面体 A'-BCD的体积为 $\frac{1}{3}$ | ||
| C. | CA'与平面 A'BD所成的角为 30° | D. | ∠BA'C=90° |
2.函数f(x)=log2$\frac{x}{2}$•log2$\frac{x}{4}$,x∈(2,8]的值域为( )
| A. | [0,2] | B. | [-$\frac{1}{4}$,2] | C. | (0,2] | D. | (-$\frac{1}{4}$,2] |
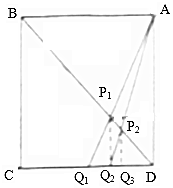 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.