题目内容
已知函数f(x)=
.
(1)求f(x)的极大值和极小值,并画出函数f(x)的草图
(2)根据函数图象,如果方程f(x)-m=0(m∈R)有且仅有两个不同的实根,求m的取值范围.
| x |
| x2+1 |
(1)求f(x)的极大值和极小值,并画出函数f(x)的草图
(2)根据函数图象,如果方程f(x)-m=0(m∈R)有且仅有两个不同的实根,求m的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:高考数学专题
分析:(1)由已知得f′(x)=
,由此利用导数性质能求出f(x)的极大值和极小值,并画出函数f(x)的草图.
(2)由(1)并根据函数图象,能求出m的取值范围.
| 1-x2 |
| (x2+1)2 |
(2)由(1)并根据函数图象,能求出m的取值范围.
解答:
解:(1)∵f(x)=
,
∴f′(x)=
,
由f′(x)=0,得x=1,或x=-1,
当x∈(-∞,-1)时,f′(x)<0;
当x∈(-1,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0,
∴f(x)的减区间为(-∞,-1),
(1,+∞),增区间为(-1,1),
∴f(x)极大值=f(1)=
,
f(x)极小值=f(-1)=-
.
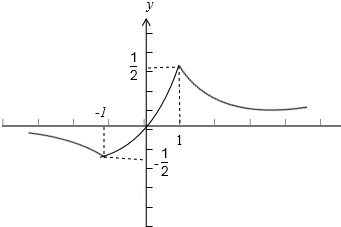
画出函数f(x)的草图如右图所示.
(2)由(1)并根据函数图象,知:
∵方程f(x)-m=0(m∈R)有且仅有两个不同的实根,
∴-
<m<0或0<m<
.
∴m的取值范围是(-
,0)∪(0,
).
| x |
| x2+1 |

∴f′(x)=
| 1-x2 |
| (x2+1)2 |
由f′(x)=0,得x=1,或x=-1,
当x∈(-∞,-1)时,f′(x)<0;
当x∈(-1,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0,
∴f(x)的减区间为(-∞,-1),
(1,+∞),增区间为(-1,1),
∴f(x)极大值=f(1)=
| 1 |
| 2 |
f(x)极小值=f(-1)=-
| 1 |
| 2 |
画出函数f(x)的草图如右图所示.
(2)由(1)并根据函数图象,知:
∵方程f(x)-m=0(m∈R)有且仅有两个不同的实根,
∴-
| 1 |
| 2 |
| 1 |
| 2 |
∴m的取值范围是(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
设向量
=(x,1),
=(4,x),则“
∥
”是“x=2”的( )
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
 如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6. 某物流公司拟建造如图所示的有底容器(不计厚度,长度单位:米),其中容器的下端为圆柱形,上端顶盖为半球形,按照设计要求容器的体积为
某物流公司拟建造如图所示的有底容器(不计厚度,长度单位:米),其中容器的下端为圆柱形,上端顶盖为半球形,按照设计要求容器的体积为