题目内容
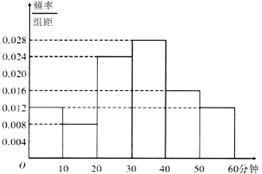 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.(I)估计该市电视观众观看“中国汉字听写大会”的日均时间的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%以上的把握认为“汉语关注者”与“是否为教育工作者”有关;
| 非汉语关注者 | 汉语关注者 | 合 计 | |
| 教育工作者 | 6 | ||
| 非教育工作者 | 30 | ||
| 合 计 | 22 |
附:k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的应用
专题:综合题,概率与统计
分析:(I)利用该组区间的中点值与频率,即可估计该市电视观众观看“中国汉字听写大会”的日均时间的平均数;
(Ⅱ)利用数据,可得2×2列联表,代入公式计算得出k2,与3.841比较即可得出结论;
(Ⅲ)从已抽取的50名电视观众中再随机抽取3人,其中“汉语关注者”的人数X服从超几何分布,可得P(X≥2)的值.
(Ⅱ)利用数据,可得2×2列联表,代入公式计算得出k2,与3.841比较即可得出结论;
(Ⅲ)从已抽取的50名电视观众中再随机抽取3人,其中“汉语关注者”的人数X服从超几何分布,可得P(X≥2)的值.
解答:
解:(I)由已知
=5×0.12+15×0.08+25×0.24×35×0.28+45×0.16+55×0.12=31.4;
(Ⅱ)由已知得;
2×2列联表中的数据代入公式计算,得k2=
≈2.652,
∵2.652<3.841,
∴没有95%以上的把握认为“汉语关注者”与“是否为教育工作者”有关;
(Ⅲ)从已抽取的50名电视观众中再随机抽取3人,其中“汉语关注者”的人数X服从超几何分布,
∴P(X≥2)=P(X=2)+P(X=3)=
+
=
.
. |
| x |
(Ⅱ)由已知得;
| 非汉语关注者 | 汉语关注者 | 合 计 | |
| 教育工作者 | 6 | 14 | 20 |
| 非教育工作者 | 16 | 14 | 30 |
| 合 计 | 22 | 28 | 50 |
| 50×(6×14-14×16)2 |
| 20×30×22×28 |
∵2.652<3.841,
∴没有95%以上的把握认为“汉语关注者”与“是否为教育工作者”有关;
(Ⅲ)从已抽取的50名电视观众中再随机抽取3人,其中“汉语关注者”的人数X服从超几何分布,
∴P(X≥2)=P(X=2)+P(X=3)=
| ||||
|
| ||
|
| 207 |
| 350 |
点评:本题考查独立性检验的运用及频率分布直方图的性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目